Homework 6

Due: See homework page
Directory name in your github repository for this homework (case sensitive): hw6

Skeleton Code

Some skeleton code has been provided for you in the hw6 folder and has been pushed to the Github repository resources. If you already have this repository locally cloned, just perform a git pull. Otherwise you’ll need to clone it.

Written Portion

Problem 0 - Complete the Course Evalutions (0%)

Take a moment and complete the course evaluations. They should be available via Blackboard. Go to the home page (not for our course but for all of Blackboard) and find the tab in the upper left labelled “Course Evaluations”. Your feedback is appreciated and helps make the class better. If there is constructive or negative feedback, consider describing an alternative approach (solution) to the problem. Thanks!

Problem 1 - Number Thoery (30%)

To receive credit for each problem, show your work in such a way that allows the grader to recognize that you understand the relevant lecture material.

Place your answers in a file nt1.pdf.

Compute $14^{37} \mod{5}$.
What is $\sum_{i=1}^{100} i! \mod{7}$?
Find the multiplicative inverse of 8 in $\mathbb{Z}_{13}$.
Find the multiplicative inverse of 83 in $\mathbb{Z}_{191}$
Solve $58*x + 26*y \equiv gcd(58,26)$. Show your work in such a way that allows the grader to recognize that you understand the relevant lecture material.
Prove that if p is prime and $p \equiv 1 \mod{5}$ then $p \equiv 1 \mod{10}$.

Programming Portion

Problem 4 - Write Your Own String Hash Function (15%)

In this problem you will write your own hash function for std::string in the provided hash.h file. While std::strings can be of arbitrary length and contain any legal ASCII character, we will assume the largest string you will ever receive is 28 letters long (e.g. antidisestablishmentarianism) and only contains letters and digits (‘0’-‘9’). For the letters, you should treat upper-case letters the same as you would lower-case letters.

The Approach

The basic approach will be to treat groups of letters/digits as base-36 and convert to an integer value (i.e. the decimal equivalent).

First translate each letter into a value between 0 and 35, where a=0, b=1, c=2, …., z=25 and digit '0'=26, … '9'=35. Be sure to convert an upper case letter to lower case before performing this mapping. Next you will translate a (sub)string of 6 letters a1 a2 a3 a4 a5 a6 into an (unsigned long long) 64-bit integer w[i] (essentially converting from base-36 to decimal), via the following mathematical formula:

\[w[i] = 36^5*a1 + 36^4*a2 + 36^3*a3 + 36^2*a4 + 36*a5 + a6\]

Place zeros in the leading positions if your (sub)string is shorter than 6 letters. So an example string like "104" would set a1, a2, and a3 all to zero (since we only have a length 3 string) and yield $36^2*27 + 36*26 + 30$ (since '1' : 27, '0' : 26, and '4' : 30) You should use the base conversion approach taught in class to avoid repeated calls to pow(). Note that indexing is a bit tricky here so think carefully. The digit at the “end” of the string is assigned the power 36^0, and the 2nd to last letter is worth 36^1, etc.

If an input word is longer than 6 letters, then you should first do the above process for the last 6 letters in the word, then repeat the process for each previous group of 6 letters. Recall, you will never receive a word longer than 28 characters. The last group may not have 6 letters in which case you would treat it as a substring of less than 6 characters as described above. Since we have at most 28 characters this process should result in a sequence of no more than 5 integers: w[0] w[1] w[2] w[3] w[4], where w[4] was produced by the last 6 letters of the word.

Store these values in an array (of unsigned long long). Place zeros in the leading positions of w[i] if the string does not contain enough characters to make use of those values. So for a string of 12 letters, w[0], w[1], and w[2] would all be 0 and only w[3] and w[4] would be (potentially) non-zero.

We will now hash the string. Use the following formula to produce and return the final hash result using the formula below (where the r values are explained below).

\[h(k) = (r[0]*w[0] + r[1]*w[1] + r[2]*w[2] + r[3]*w[3] + r[4]*w[4])\]

where the $r[i]$ values are either:

5 random numbers created when you instantiate the hash function using the current time as your seed (i.e. srand(time(0))). Be sure to #include <ctime> and #include <cstdlib>.
5 preset values for debugging (so we all get the same hash results): r[0]=983132572, r[1]=62337998, r[2]=552714139, r[3]=984953261, r[4]=261934300 (these numbers were generated by random.org)

Note: We will allow h(k) to produce a large integer (beyond the range of m, the table size) and only mod it by the table size in the hash table (see other programming problem).

The constructor of your hash object will take a debug parameter, which, if true should set the r values to the above debugging values, and if false should select the ranomized values.

Note: Make sure you compute using unsigned long long variables or cast (constants or other variables) to that type at the appropriate places so that you don’t have an overflow error.

Testing

We have provided a simple test program, str-hash-test.cpp where you can provide a string on the command line and it will hash the string and output the hash result. Below is some debug output of the w[i] values computed for several test strings using the debug r values.

Below is the output for a few strings:

./str-hash-test abc

yields

w[0] = 0
w[1] = 0
w[2] = 0
w[3] = 0
w[4] = 38
h(abc)=9953503400

./str-hash-test abc123

yields

w[0] = 0
w[1] = 0
w[2] = 0
w[3] = 0
w[4] = 1808957
h(abc123)=473827885525100

./str-hash-test-sol B

yields

w[0] = 0
w[1] = 0
w[2] = 0
w[3] = 0
w[4] = 1
h(B)=261934300

./str-hash-test-sol gfedcba

yields

w[0] = 0
w[1] = 0
w[2] = 0
w[3] = 6
w[4] = 309191940
h(gfedcba)=80987980279261566

./str-hash-test antidisestablishmentarianism

yields

w[0] = 17540
w[1] = 195681115
w[2] = 2203855
w[3] = 732943745
w[4] = 484346964
h(antidisestablishmentarianism)=1137429692708383810

Problem 2 - Hash Table with Quadratic Probing (35%)

You will create a HashTable data structure that uses open-addressing (i.e. uses probing for collision resolution) and NOT chaining. Your table should support linear and quadratic probing via functors. Initially, we will use the std::hash<> functor provided with the C++ std library. In a future question, you will implement your own hash function for strings made of letters and digits only (no punctuation). You should complete the implementation in ht.h.

template<
    typename K, 
    typename V, 
    typename Prober = LinearProber,
    typename Hash = std::hash<K>, 
    typename KEqual = std::equal_to<K> >
class HashTable
{
    /* Implementation */
};

The template types are as follows:

K: the key type (just like a normal map)
V: the value type (just like a normal map)
Prober: a functor that supports an init() and next() function that the hash table can use to generate the probing sequence (e.g. linear, quadratic, double-hashing). A base Prober class has been written and a derived LinearProber is nearly complete. You will then write your own QuadraticProber class to implement quadratic probing.
Hash: The hash function that converts a value of type K to a std::size_t which we have typedef’d as HASH_INDEX_T.
KEqual: A functor that takes two K type objects and should return true if the two objects are equal and false, otherwise.

Internally, we will use a hash table of pointers to HashItems, which have the following members:

typedef std::pair<KeyType, ValueType> ItemType;
struct HashItem {
        ItemType item;  // key, value pair
        bool deleted;
};

You should allocate a HashItem when inserting and free them at an appropriate time based on the description below. If no location is available to insert the item, you should throw std::logic_error.

We have also provided a constant array of prime sizes that can be used, in turn, when resizing and rehashing is necessary. This sequence is: 11, 23, 47, 97, 197, 397, 797, 1597, 3203, 6421, 12853, 25717, 51437, 102877, 205759, 411527, 823117, 1646237, 3292489, 6584983, 13169977, 26339969, 52679969, 105359969, 210719881, 421439783, 842879579, 1685759167. Thus, when a HashTable is constructed it should start with a size of 11. The client will supply a loading factor, alpha, at construction, and before inserting any new element, you should resize (to the next larger size in the list above) if the current loading factor is at or above the given alpha.

For removal of keys, we will use a deferred strategy of simply marking an item as “deleted” using a bool value. These values should not be considered when calls are made to find or operator[] but should continue to count toward the loading factor until the next resize/rehash. At that point, when you resize, you will only rehash the non-deleted items and (permanently) remove the deleted items.

We will not ask you to implement an iterator for the hash table. So find() will simply return a pointer to the key,value pair if it exists and nullptr if it does not.

To facilitate tracking relevant statistics we will use for performance measurements, we have provided the core probing routine: probe(key). This routine, applies the hash function to get a starting index, then initializes the prober and repeatedly calls next() until it finds the desired key, reaches a hashtable location that contains nullptr (where a new item may be inserted if desired), or reaches its upper limit of calls (i.e. cannot find a null location). probe() utilizes the Prober. Prober::init is called to give the prober all relevant info that it may need, regardless of the probing strategy (i.e. starting index, table size, etc.). Then a sequence of calls to Prober::next() will ensue. If, for example we are using linear probing, the first call to next() would yield h(k), the subsequent call to next() would yield h(k)+1, the third call would yield h(k)+2, etc. Notice: the first call to next() just returns the h(k) value passed to Prober::init(). As probing progresses we will update statistics such as the total number of probes. Some accessor and mutator functions are provided to access those statistics.

Note: When probing to insert a new key, we could stop on a location marked as deleted and simply overwrite it with the key to be inserted. However, because our design uses the same probe(key) function for all three operations: insert, find, and remove, and certainly for find and remove we would NOT want to stop on a deleted item, but instead keep probing to find the desired key, we will simply take the more inefficient probing approach of not reusing locations marked for deletion when probing for insertion.

A debug function, reportAll is also provided to print out each key value pair. Use this when necessary to help you debug your code.

Probers

We have abstracted the probing sequence so various strategies may be implemented without the hash table implementation being modified. Complete the LinearProber and then write a similar QuadraticProber that uses quadratic probing. Recall that if a prime table size is used, insertion using quadratic probing is only guaranteed to find a free location if the loading factor is less than or equal to m/2. Thus after m/2 probes, return npos.

Testing Your Hash Table

A simple test driver program ht-test.cpp has been provided which you may modify to test various aspects of your hash table implementation. We will not grade this file so use it as you please.

Problem 5 - Subgraph Isomorphism (20%)

In this problem, you will again use backtracking search to determine if two graphs are isomorphic. Two graphs, $G1$ and $G2$, are said to be isomorphic if:

There exists a bijection (1-to-1), or mapping $M$, from the vertices of G1 onto the vertices of G2 where M(v1) => v2 for v1 in G1 and v2 in G2), such that:
- for each edge $(u1,v1)$ in G1, the edge $(M(u1), M(v1))$ exists in G2 AND
- for each vertex, $v1$ in G1, $deg(v1) = deg(M(v1))$.

We have written and implemented a basic graph class for you. It reads in graphs (as adjacency lists) from an input stream (file) and allows you to check if an edge exists, find all the neighbors of a given vertex, and get all the vertices in the graph. It uses a std::map to store the graph information in adjancency list form.

// Graph class for use with graph isomorphism function
typedef std::string VERTEX_T;
typedef std::set<VERTEX_T> VERTEX_SET_T;
typedef std::vector<VERTEX_T> VERTEX_LIST_T;
class Graph {
public:
    Graph(std::istream& istr);
    bool edgeExists(const VERTEX_T& u, const VERTEX_T& v) const;
    const VERTEX_SET_T& neighbors(const VERTEX_T& v) const;
    VERTEX_LIST_T vertices() const;
private:
    std::map<std::string, VERTEX_SET_T > adj_;
};

Your task is to write a function (prototyped below) to determine if the two graphs are isomorphic (as defined above) and return true if so, and false, otherwise, AND if you return true you must also provide the valid mapping of vertices in graph 1 and their corresponding mapped vertices in graph 2 that form the isomorphism (i.e. you should produce a map where each key represents a vertex v1 in G1 and its corresponding value represents a vertex, v2, in G2 that v1 maps onto).

To create, update, and store this mapping, you MUST use your hash table data structure from the previous part of this homework. If you do not use your hash table implementation, you will RECEIVE NO CREDIT on this problem.

/// Use your hashtable for the mapping between vertices
typedef HashTable<VERTEX_T, VERTEX_T> VERTEX_ID_MAP_T;

/**
 * @brief Determines if two graphs are isomorphic
 * 
 * @param g1 Graph 1
 * @param g2 Graph 2
 * @param mapping isomorphic mapping between vertices of graph 1 (key) and graph 2 (value)
 * @return true If the two graphs are isomorphic
 * @return false Otherwise
 */
bool graphIso(  const Graph& g1, 
                const Graph& g2, 
                VERTEX_ID_MAP_T& mapping);

Testing

We have provided a “driver”/test program (graphiso-driver.cpp) that will read in two files (whose names are given on the command line) that contain graph descriptions, call your function, and then print the results for you to verify. You can compile it with make and run it as:

./graphiso-driver graph1a.in graph1b.in

Use graphiso-driver to do some sanity tests of your code before moving on to any of the tests from our grading suite.

A few examples of graphs and the results that your function should produce are shown below. We have provided three pairs of graphs in the files: graph1a/b.in, graph2a/b.in, and graph3a/b.in that match the examples shown below.

Graph 1a/1b:

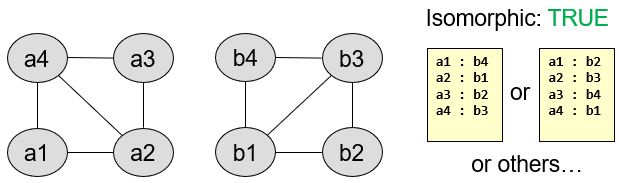
drawing

Graph 2a/2b:

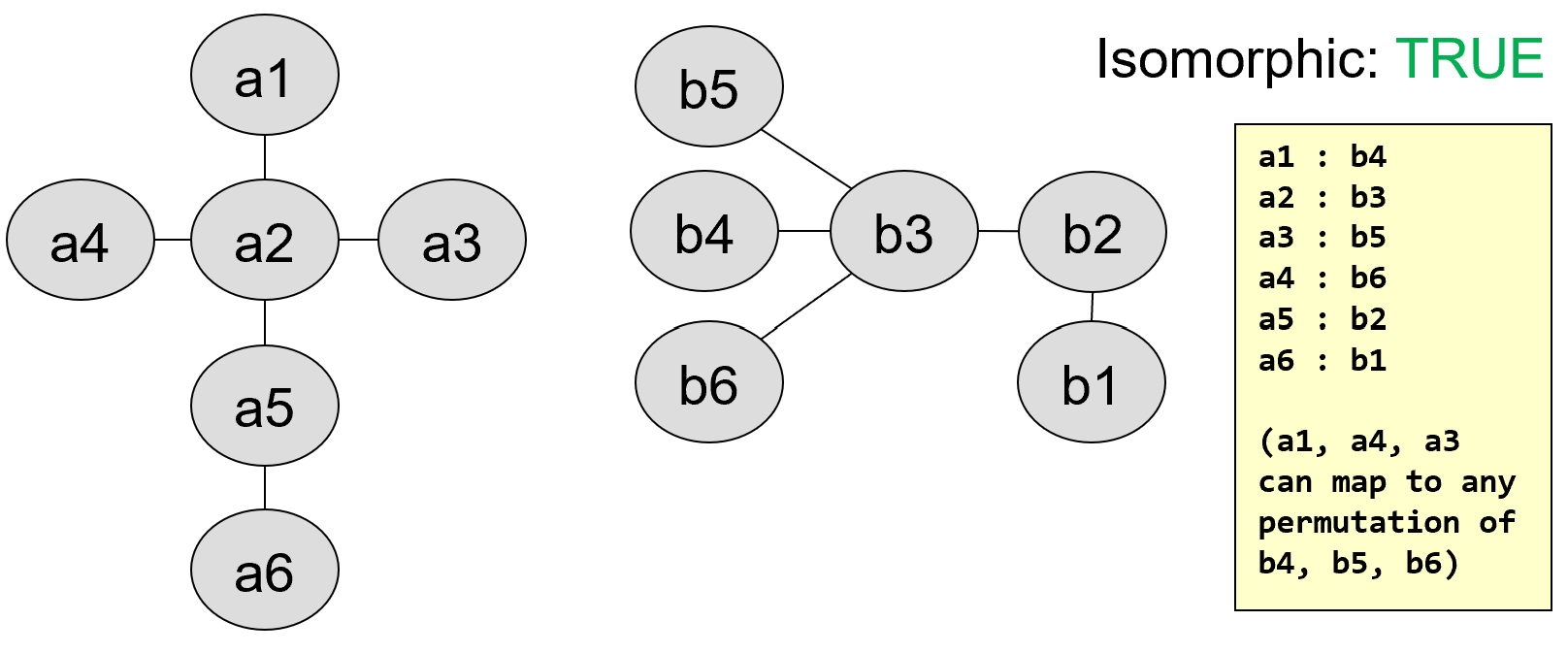
drawing

Graph 3a/3b:

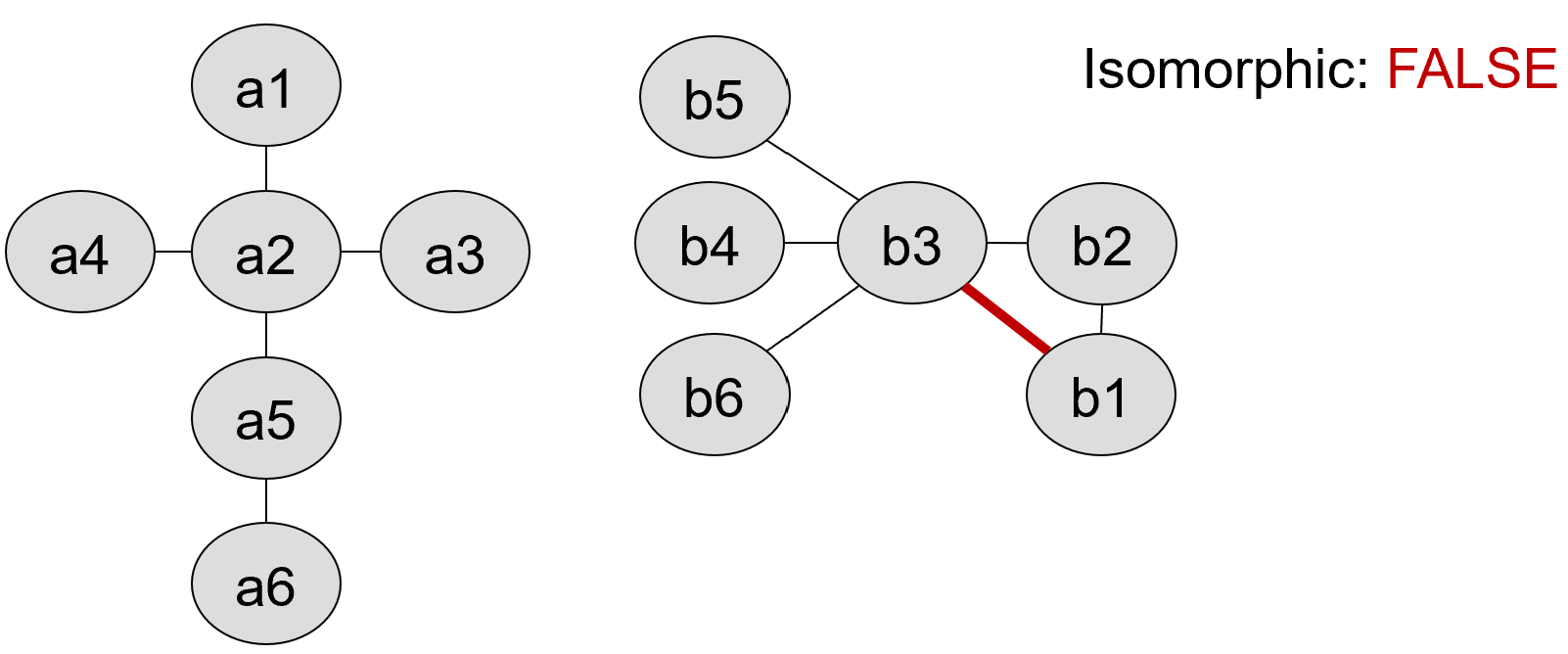
drawing

During grading, we will run some additional instructor tests but they will be similar to the ones we provide in our test suite.

Requirements and Assumptions

As always you may not change the signature of the primary function provided.
You MAY define helper functions in graphiso.cpp
You MUST use a recursive approach that follows the general backtracking structure presented in class. Failure to use such a recursive approach will lead to a 0 on this part of the assignment.
You MAY use structures such as std::set or std::map or std::vector as necessary to help your implementation.
There is no specific runtime, but you must pass each test in ctest with timeout limits of 60 seconds per test.
Any valid mapping is acceptable (since many may exist for certain graphs). Our tests simply verify your solution rather than looking for a hard-coded mapping.

Hints and Approach

Recall that a backtracking search algorithm is a recursive algorithm that is similar to generating all combinations, but skipping the recursion and moving on to another option if the current option violates any of the constraints. It is likely easiest to recurse over each vertex in graph 1 attempting to find a suitable mapping to a vertex in graph 2 that meets the criteria known (or assigned) at the current time. As you map a vertex from G1 to G2, you can check whether the vertices you’ve mapped are “consistent” and meet the isomorphism requirements. Because not all vertices will be mapped during the intermediate stages of your algorithm, you can only determine if a mapping is NOT valid by finding mapped vertices that have differing degrees or if an edge, $(u1, v1)$, in G1 where both $u1$ and $v1$ are mapped to a vertex in G2, does NOT have a corresponding edge $(M(u1), M(v1))$ in G2.

We have provided the start of a helper function you can use to implement these checks.

bool isConsistent(const Graph& g1, const Graph& g2, VERTEX_ID_MAP_T& mapping);

You should consider completing it and calling it from your main backtracking code.

Submission Files

Ensure you add/commit/push all your source code files, Makefile, and written problem files. Do NOT commit/push any test suite folder/files that we provide from any folder other than the resources/hw6 repo. Then submit your SHA on our submission site.

Please note we may run additional instructor tests for the coding problems that will affect your grade. They will be similar in style to the provided test suite, but we do so to ensure you do not hard-code solutions to specific tests.

WAIT You aren’t done yet. Complete the last section below to ensure you’ve committed all your code.

Commit then Re-clone your Repository

Be sure to add, commit, and push your code in your hw6 directory to your hw-username repository. Now double-check what you’ve committed, by following the directions below (failure to do so may result in point deductions):

In your terminal, cd to the folder that has your resources and hw-username
Create a verify-hw6 directory: $ mkdir verify-hw6
Go into that directory: $ cd verify-hw6
Clone your hw_username repo: $ git clone git@github.com:/hw-username.git
Go into your hw6 folder $ cd hw-username/hw6
Switch over to a docker shell, navigate to the same verify-hw6/hw-username/hw6 folder.
Recompile and rerun your programs and tests to ensure that what you submitted works. You may need to copy over a test-suite folder from the resources repo, if one was provided.