Homework 4

• Due: See homework page
• Directory name in your github repository for this homework (case sensitive): hw4

Skeleton Code

Some skeleton code has been provided for you in the hw4 folder and has been pushed to the Github repository resources. If you already have this repository locally cloned, just perform a git pull. Otherwise you’ll need to clone it.

Written Portion

Problem 1 - AVL Operations (10%)

Consider the following initial configuration of an AVL Tree:

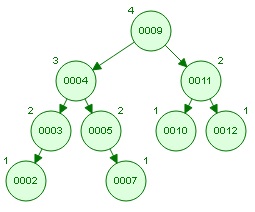
Draw the tree representation of the AVL tree after each of the following operations, using the method presented in class (when deleting, always promote a value from the right subtree…your successor). Your operations are done in sequence, so your tree should have 9 values in it when you’re done. Make sure to clearly indicate each of your final answers.

• Remove 10
• Insert 13
• Insert 6
• Remove 9
• Insert 14
• Remove 11

We highly recommend you try to solve these by hand before using any tools to verify your answers.

Put your answers in a PDF file named: q1.pdf

Programming Portion

Problem 2 - Tree Traversals (10%)

Write a recursive (no loops allowed) routine to count the number of nodes in a binary search tree of integers whose keys are between [min, max] (inclusive) and above a depth, d in the tree.

The tree nodes are instances of the following struct:

struct Node {
    int key;
    Node *left, *right, *parent;
};

The function is prototyped in internal-range.h and should be implemented in the corresponding .cpp file.

// Prototype
int sumInternalRange(Node * root, int depth, int min, int max);

For example, given the BST:

Examples

Given the tree:

  4
 / \
3   5
     \
      6

• A call to sumInternalRange(root, 2, 3, 4) should return 2 since nodes 3, 4, and 5 are above depth 2 (but 6 is not) and nodes 3 and 4 are in the inclusive range: [3,4].

• A call to sumInternalRange(root, 1, 3, 4) should return 1 since only the root is at a depth (i.e. 0) above d=1 and in the range.

• A call to sumInternalRange(root, 1, 0, 3) should return 0 since only the root is at a depth (i.e. 0) above d=1 but the root’s value is not in the range [0,3].

You MAY define helper functions if needed in internal-range.cpp. We have also provided a VERY RUDIMENTARY test program internal-range-test.cpp that you may use and modify as desired to test certain configurations and debug your code. It will not be graded.

Problem 3 - BSTs and Iterators (35%)

Important Perspective: Remember that BSTs are an implementation of the set and map ADT. While a set only has keys, a map has a value associated with each key. But in any map or set, it is the key that is used to organize and lookup data in the structure and thus must be unique.

In this homework you will implement a binary search trees and then extend it to build an AVL tree.

We are providing for you a half-finished file bst.h (in the resources repository) which implements a simple binary search tree. We are also providing a complete print_bst.h file that allows you to visually see your tree, for help in debugging. HOWEVER to use this print function you must have a working iterator implementation. If the tree doesn’t print correctly you need to verify your iterator works and also that your insertions/removals haven’t destroyed parts of the tree. This file is already #include‘d into your bst.h and is invoked by simply calling the public print() member function on your tree (e.g. if you are in main() and have a BST object named b, then just call b.print();).

You will need to complete the implementation for all seven functions that have TODO next to their declaration in bst.h. We provide additional clarifications for the following functions, where n is the number of nodes in the tree, and h is the height of the tree:

1. void insert(const std::pair<const Key, Value>& keyValuePair) : This function will insert a new node into the tree with the specified key and value. There is no guarantee the tree is balanced before or after the insertion. If key is already in the tree, you should overwrite the current value with the updated value. Runtime is O(h).
2. void remove(const Key& key) : This function will remove the node with the specified key from the tree. There is no guarantee the tree is balanced before or after the removal. If the key is not already in the tree, this function will do nothing. If the node to be removed has two children, swap with its predecessor (not its successor) in the BST removal algorithm. If the node to be removed has exactly one child, you can promote the child. You may NOT just swap key,value pairs. You must swap the actual nodes by changing pointers, but we have given you a helper function to do this in the BST class: swapNode(). Runtime of removal should be O(h).
3. void clear() : Deletes all nodes inside the tree, resetting it to the empty tree. Runtime is O(n).
4. Node* internalFind(const Key& key) : Returns a pointer to the node with the specified key. Runtime is O(h).
5. Node* getSmallestNode() : Returns a pointer to the node with the smallest key. This function is used by the iterator. Runtime is O(h).
6. bool isBalanced() const : Returns true if the BST is an AVL Tree (that is, for every node, the height of its left subtree is within 1 of the height of its right subtree). It is okay if your algorithm is not particularly efficient, as long as it is not O(n^2). This function may help you debug your AVL Tree in the next part of this problem, but it is mainly given as practice of writing recursive tree traversal algorithms. Think about how a pre- or post-order traversal can help.
7. Constructor and destructor : Your destructor will probably just call the clear function. The constructor should take constant time.
8. You will need to implement the unfinished functions of the iterator class. Note: You do NOT need to check whether the iterator is about to dereference a NULL pointer in operator*() or operator->() of the iterator. Just let it fault. It is up to the user to ensure the iterator is not equal to the end() iterator.

Notes:

• Remember a BST (as well as any map implementation) should always be organized via the key of the key/value pair.

• The iterator class you write is mainly for clients to call and use to access the key,value pairs and traverse the tree. You should not use it as a helper to traverse the tree intenally. Instead use Node<K,V>* or AVLNode<K,V>* pointers directly along with internalFind, successor, predecessor etc.

• In this class we make use of static member functions. You can search online for what this means but here is a brief summary. A static member function cannot be called upon an object ( bst.static_member_func() ) and DOES NOT have a this pointer. Thus in that function you cannot try to access this->root_. Essentially, it is like a global level function shared by all instances of BSTs. It is a member of the class so if someone passes in an actual BST it CAN access private data (i.e. BST’s root_ member). We have made predecessor() a static member function and we suggest you make a static successor() function. That will be useful so that the iterator class can just call successor() when we want to increment the iterator. We use static for successor because the iterator class doesn’t have a BST pointer/reference so it couldn’t call successor if it was a normal member function.

• Very Important Warning: Please do not remove, modify, or rename any of the members (public, protected, OR private) in bst.h. You may add protected or private helper functions. protected helper functions may be useful if the AVLTree class you will code in the latter problem will also benefit from that function. If you do not heed this warning, our tests won’t work, and you’ll lose points.

• Reminder: If the tree doesn’t print correctly in your test program(s), you need to verify your iterator works (e.g. successor()) and also that your insertions/removals haven’t destroyed parts of the tree.

Problem 4 - AVL Trees (45%)

We are providing you a half-finished file avlbst.h (in the homework-resources repository) for implementing an AVL Tree. It builds on the file you completed for the previous question.

Complete this file by implementing the insert() and remove() functions for AVL Trees. You are strongly encouraged to use private/protected helper functions.

When you compile code that includes avlbst. you will need to add the option --std=c++11 to the g++ compilation command. This is because of the usage of the override keyword for various virtual functions. You can read about it online but it mainly provides some additional compiler checks to ensure the signatures of a virtual function in the derived class matches the one you are attempting to “override” in the base class (i.e. if your base virtual function is a const-member but you forget to add const to the derived and thus are creating a whole new member function, the compiler will catch the error).

Related Videos

• A video walkthrough is available and demonstrates techniques that can be used to debug either your BST or AVL tree.

Notes and Requirements

1. You know this one already, but you are NOT allowed to use online sources to give you the game plan for coding an AVL tree. Feel free, however, to ask various questions on Piazza, utilize course materials, or ask in office hours.
2. For the insert() method, you should handle duplicate entries by overwriting the current value with the updated value.
3. There is a data member variable balance_ for the AVLNode in avlbst.h which you should use to store and updated the balance of a given node. It is a char type to save memory because it only needs to represent -2, -1, 0, 1, or 2. A full 32-bit int is unnecessary. Note that you can assign integers to a char (e.g. char b = -2) it’s just that the char is 8-bits and thus has a range of -128 to +127. One issue is if you cout that char, you need to cast it to an int, because operator<< will try to interpret a char variable as an ASCII char (which would yield garbage) when you want to see the integer value of that char.
4. When writing a class (AVLTree) that is derived from a templated class (BinarySearchTree), accessing the inherited members must be done by scoping (i.e. BinarySearchTree<Key,Value>:: or preceding with the keyword this->.
5. This note may not make sense until you have started coding. Your AVLTree will inherit from your BST. This means the root member of BST is a Node type pointer that points to an AVLNode (since you will need to create AVLNodes with balance values for your AVLTree), which is fine because a base Node pointer can point at derived AVLNodes. If you need to access AVLNode-specific members (i.e., members that are part of AVLNode but not Node) then one simple way is to (down)cast your Node pointer to an AVLNode pointer, as in static_cast<AVLNode<K,V>*>(root) to temporarily access the AVLNode-specific behavior/data.
6. When erasing (removing) a key that has 2 children, you should always swap it with its predecessor. Again, you must swap the nodes positions in the tree and CANNOT just swap the key/value pair data. Again, use the provided swapNode function to help you.
7. Your AVL implementation must maintain the balance of the tree and provide O(log n) runtime for insert, remove, and find. Failure to do so could lead to severe point deductions on this problem.
8. We have started a simple bst-test.cpp test program where you can test your BST and AVLTree. We will NOT grade its contents but it should at least create a BST and a separate AVLTree so that we can test your compilation when you submit. It should at least call insert, remove, and find on each of the two trees. Also having this small test that you can use to debug your code will be much easier than trying to debug with the large tests that we provide. Start by using it to do basic sanity checks on your code and only use our provided tests once you have confidence your code works.

Tips

• Helper functions like: rotateLeft(...) and rotateRight(...) are a great idea. Even simple ones like isLeftChild(n, p) or isRightChild(n,p, etc. are fine. Anything that makes it easier to abstract (and thus ensure correctness) the algorithm.

• Using gdb will be of more use on this homework more than any other. Having a small test program (your own .cpp with a main()) that does a sequence of operations that you want to check will be helpful. Then you can set a breakpoint at an operation and then step through it. Or if you are concerned about a certain operation you can set a breakpoint at the start of a function like rotateRight() or rotateLeft() and step through it. It may seem painful but we suggest getting a piece of paper, drawing some node and using gdb to print out the pointers n, n->left, n->right, n->parent, and similarly for the parent and potentially grandparent node. Once you know all the addresses, step through your code in gdb and print out the update values of these pointers and make sure it is correct!

• If the output of printBST is off it is likely that your tree’s pointers have been mangled somehow by your code OR that your iterator doesn’t work correctly. Start there to ensure things work.

Testing

We will post BST and AVL tests in the resources repo. Feel free to use them for more in-depth testing once you have some confidence things seem to be working. We do NOT recommend starting your testing with these. They may be too much to debug initially. Write your own test .cpp and do some basic operations on samll trees to ensure those work before running the more exhaustive tests that we provide.

Checkpoint

For checkpoint credit, submit your working code for the BST/iterator implementation (though not necessarily the AVL tree). Ensure you add/commit/push your hw-username repo with a hw4 subfolder that contains:

• bst.h, print_bst.h (it’s fine to include your other source files like avlbst.h, Makefile, bst-test.cpp)
• THEN you must submit your SHA on our Submit page linked from the Homework Page.

We will use hw4_tests/bst_tests/bst_tests for the checkpoint. They must compile, run, and pass all tests with no valgrind or other memory errors. Failure to pass even one test or having 1 valgrind error will result in 0 credit for the checkpoint. It is fine to push input test files if you like, though we will not grade them.

Submission Files

Ensure you add/commit/push all your source code files, Makefile, and written problem files. Do NOT commit/push any test suite folder/files that we provide from any folder other than the resources/hw4 repo. Then submit your SHA on our submission site.

WAIT You aren’t done yet. Complete the last section below to ensure you’ve committed all your code.

Commit then Re-clone your Repository

Be sure to add, commit, and push your code in your hw4 directory to your hw-username repository. Now double-check what you’ve committed, by following the directions below (failure to do so may result in point deductions):

1. In your terminal, cd to the folder that has your resources and hw-username
2. Create a verify-hw4 directory: $ mkdir verify-hw4
3. Go into that directory: $ cd verify-hw4
4. Clone your hw_username repo: $ git clone git@github.com:/hw-username.git
5. Go into your hw4 folder $ cd hw-username/hw4
6. Switch over to a docker shell, navigate to the same verify-hw4/hw-username/hw4 folder.
7. Recompile and rerun your programs and tests to ensure that what you submitted works. You may need to copy over a test-suite folder from the resources repo, if one was provided.