Due at the end of your registered lab section.

Hashtables

1 - What is a Map?

Recall that a map is a data structure used mostly for fast look ups or searching data. It stores data in the form of key, value pairs, where every key is unique. Each key maps to a value, hence the name “map.”

The look up speed and ordering of map elements depends on the data structure we use to implement our map. Generally, we’ve learned in past lectures that lookup is an O(logn) function, assuming we use a tree structure to organize the underlying data. But what if we wanted this lookup operation to be faster? Is there an underlying data structure that could allow for constant time access?

2 - Let’s Talk About Hash Tables

A Hash Table is like an array in many aspects. However, in order to find the index in the array, we use a special function called a hash function. This converts the input into an index location that the input is then stored into.

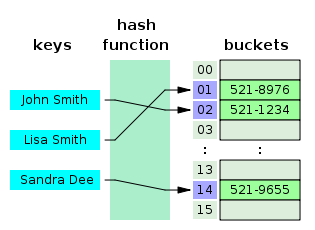
In the above example, we can see that our hash table stores strings, and those strings are stored in locations within an array specified by the hash function.

This type of data structure is very useful in terms of accessing data. You could probably think of different applications of this data structure. Maybe a set? Given an input, we first hash it, then look to see if it is inserted in our hash table by checking the index returned by our hash function. Since hashing is just a function, it takes O(1) time. If we have a good hash function that distributes keys uniformly around the table such that there are a small number of keys at each location, the entire check is O(1) on average.

There are many different applications of this type of data structure, including sets, maps, and associative arrays (which are pretty much maps).

2.1 - Hash Functions

So the whole idea of a hash table relies on the hash function. A hash function is a function that converts an object into an index location within our array.

What goals should our hash function have?

1. Easy and fast to compute
2. Uniformly distributes keys across the hash table

The first thing we want is for the function to be fast. It should be an easy calculation that takes O(1) time to compute.

Lets first go over a bad example:

int hash(int data) {
    return 42 % size;
}

This hash function is super fast. It literally just does one operation and then returns. However, it always returns the same number. This means that we are always going to go to the same array index. This doesn’t make sense. Shouldn’t our hash function result in different outputs with different inputs?

A good example of this would be:

int hash(int data){
    return 31 * 54059 ^ (data * 76963) % size;
}

Wow, I literally have no idea what the number is going to be! In this example, the output hash will likely be different for the majority of cases. It may be more operations than our first hash function, but it still does a constant amount of work. Now it also accomplishes our second goal of uniformly distributing keys, since it’s very likely that different inputs will result in different outputs.

Finally, an important note is that even though we want hashtables to have a good distribution over the size of our hashtable, it must always be deterministic. This means that if we pass the hash function the same input multiple times, it will always result in the same output. This means no random number generators! It’s critical that a hash function is deterministic because if we ever need to lookup a value in our hashtable, then we need to find where we put it!

2.2 - Collisions

So what happens if the hash function outputs the same index for multiple objects? This is called a collision. In general, collisions are not completely avoidable, so we will need ways to handle them. There are two approaches:

• open addressing such as linear probing, quadratic probing, or double hashing.
• closed addressing such as chaining or buckets.

2.3 - Open Addressing

The idea with open addressing is that every location in the array can only have 1 thing in it. This means that we will have to find a free spot that we can place the object in. Linear probing is a very simple solution.

Linear probing is where you just keep incrementing up/looking at the next index until you find a free location.

The algorithm for inserting into a linear probed hashtable is:

1. Hash the element, which gives you a position in the table.
2. If the position is already taken, try the next position (if you reach the end of the table, wrap back to the start).
3. Repeat step 2 until you have found an empty spot.
4. Insert the element at that empty spot.

The algorithm for finding a key in a linear probed hashtable is:

1. Hash the key you want to find, which gives you a position in the table.
2. If the position contains a key, compare it with the key you want to search. If they are equal, you’ve found the key; otherwise, move to the next position. If the position is empty (i.e does not contain a key), you know that the key does not exist in the table.
3. Repeat step 2 until the algorithm terminates.

Removing from the hashtable is a little bit more involved:

1. First find the position of the key with the method illustrated above.
2. Delete the key there.
3. Move to the next position. If it is not empty, delete the key there and reinsert it.
4. Repeat step 3 until you have reached an empty spot or you have looped back to the position you found in step 1.

Here is an example for you to practice with:

Suppose you have three keys with the following hash:

• Key A has hash 0
• Key B has hash 1
• Key C has hash 1
• Key D has hash 1
• Key E has hash 2

And you have a hash table of size 5.

Try yourself with pen and paper. What will the hashtable look like following each of those steps (in sequence):

• Insert B
• Insert C
• Insert E
• Insert A
• Insert D
• Remove B
• Remove E

2.4 - Chaining

For closed addressing we will focus on chaining. Chaining allows for multiple objects to reside within the same array location. The array is changed to be an array of lists or some other data structure, allowing us to store multiple items per index. We often use an array of linked lists, hence the name “chaining.”

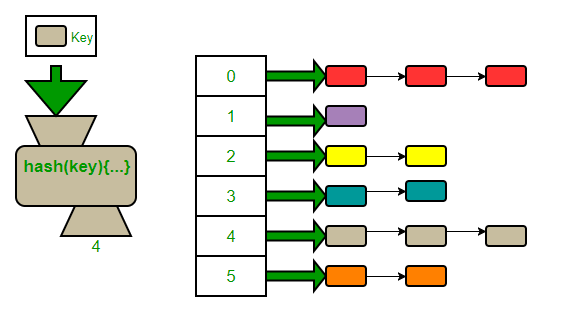
Other implementations may use another type of list or even a balanced tree.

Because chaining allows for buckets, it is probable for n objects to all be placed within the same bucket. The worst case runtime is O(n). Chaining may even prevent our goal of O(1) on average. However, a scenario like this should not occur if the hash function is good and the size of the hash table is big enough.

3 - OrderedMap vs. UnorderedMap

So let’s see a real life example of a hash table.

3.1 - OrderedMap

An ordered map uses a balanced binary search tree as its underlying data structure. We haven’t gone over it in lecture yet, but for now, it is sufficiently to know that it is used in the implementation of std::map (it usually uses a version of balanced binary search tree called a Red-Black Tree), and it has the time complexity of:

1. find(key)

   O(logn)

2. insert(key, value)

   O(logn)

3. remove(key)

   O(logn)

It is called a “ordered map” because doing an in-order traversal of a binary search tree would give you an ordered traversal of all the keys in the map (ex. if the keys strings, they would be printed in alphabetical order).

3.2 - UnorderedMap

An unordered map uses a hash table as its underlying data structure. This means that access operations are O(1) on average, but because of this, no order can be inferred. By improving the runtime of operations, we had to sacrifice the ordering property.

You must explicitly create an unordered map using std::unordered_map.

1. find(key)

   O(1) on average

2. insert(key, value)

   O(1) on average

3. remove(key)

   O(1) on average

4 - HashTable Assignment

You will be implementing an unordered set with string keys using linear probing. The hash function is already implemented so you will be using the array of vector pointers to do the required functions.

To run the tests, run make to compile the hashtable binary, then run the program. It should print out all “Good”, and of course not segfault or anything.

• Implement remove in hashtable.cpp
• Show your passing tests to a TA/CP for checkoff!

NOTE: as a bonus, there is an optional, commented-out test called TestRemoveSUPERSTRESS_AGHHHHHHHHH. If you’ve implemented everything correctly, you should be able to run this test pretty quickly! Otherwise, it takes a very long time to run (though you might have success running the HashtableTest executable faster without Valgrind.) Regardless, you do not need to wait for/pass this test to pass to get checked off!