Due at the end of your registered lab section. Remember to get checked off for last week’s asynchronous lab as well!

Maintaining the BST and Height-Balancing Properties

While you are learning about AVL trees in lecture, our goal for this lab is to get you as familiar with AVL trees as possible before the absolute monster that is PA6 (not to scare you sorry hehe)!

AVL trees are a type of binary search tree, and maintain the BST property through smart insertion and deletion. In an insert, you traverse the tree based on the key to be inserted. Once you encounter a situation where you can’t traverse any further, you know that the key can be placed there. Because we are traversing based on the key value, we are inherently upholding the BST property.

The same thing can be said about a deletion in a BST. This is done by choosing which node to promote. Either the predecessor, if the node has two children, or the child if the node has 1 child. By doing this, the BST property is being maintained.

The thing that is special about AVL trees is that they are self-balancing.

A self-balancing BST is a BST that maintains its balance throughout all insertions and deletions. These types of trees that auto-balance or self balance inherently with the insertion are called Self-Balancing Binary Search Trees. Other examples of these trees are:

  1. AVL Trees (as you know)
  2. Splay Trees
  3. Red Black Trees
  4. B-Trees
  5. 2-3 Trees

For all of these self-balancing binary search trees, the height-balancing property is upheld by the nature of an insert or remove. The best way to do so is with rotation, or series of rotations. We’re going to briefly review how those rotations work below.

1 - Rotations

A rotation changes the local structure of a binary tree without changing its ordering. This means that in between rotations, the BST property is still maintained.

Rotations can be broken up into left and right rotations which are just inversions of each other.

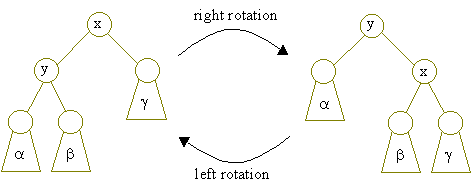
rotations

Rotaions make up the foundation of the AVL tree. In your upcoming PA6, you will need to implement these rotations in a variety of scenarios. There are 4 combinations of rotations: left-left, left-right, right-left, right-right. Sometimes, these rotations are referred to as “zig zig” or “zig zag”, or something similar. The point is, during these sequences of rotations, the tree becomes more balanced than it was before.

If longer subtrees are left and then left (left-left, or zig-zig)

T1, T2, T3 and T4 are subtrees.
         z                                      y
        / \                                   /   \
       y   T4      Right Rotate (z)          x      z
      / \          - - - - - - - - ->      /  \    /  \
     x   T3                               T1  T2  T3  T4
    / \
  T1   T2

If longer subtrees are left and then right (left-right, or zig-zag)

     z                               z                           x
    / \                            /   \                        /  \
   y   T4  Left Rotate (y)        x    T4  Right Rotate(z)    y      z
  / \      - - - - - - - - ->    /  \      - - - - - - - ->  / \    / \
T1   x                          y    T3                    T1  T2 T3  T4
    / \                        / \
  T2   T3                    T1   T2

If longer subtrees are right and then right (right-right, or zig-zig)

  z                                y
 /  \                            /   \
T1   y     Left Rotate(z)       z      x
    /  \   - - - - - - - ->    / \    / \
   T2   x                     T1  T2 T3  T4
       / \
     T3  T4

If longer subtrees are right and then left (right-left, or zig-zag)

   z                            z                            x
  / \                          / \                          /  \
T1   y   Right Rotate (y)    T1   x      Left Rotate(z)   z      y
    / \  - - - - - - - - ->     /  \   - - - - - - - ->  / \    / \
   x   T4                      T2   y                  T1  T2  T3  T4
  / \                              /  \
T2   T3                           T3   T4

By using combinations of rotations during insertion and removal, we are able to maintain consistent balance throughout the lifetime of the tree.

2 - Inserting

During insertion, we start by inserting the value at its correct location as a normal BST would. Then, we traverse up the tree, evaluating the local height of each node and fixing that portion if the height of the left and right subtrees differ by 2 or more. We only need to traverse up the tree from the inserted node because the subtree containing the new node is the only subtree where height can change and we need to rotate.

We fix the tree beginning with the newly inserted node.

3 - Removing

During removal, we remove as normal and then proceed to fix the tree by traversing up, starting with the parent of the deleted node. The process of checking balanace and fixing height is the same as outlined in the insertion part.

4 - Exercise

Take some time to confirm your understanding by showing the tree after each of the following operations in a new file named lab8-avl.txt.

Initial Tree

                13
        +--------+---+
        10          15
    +---+---+        +--+
    5       11          16
+---+---+
4       8

Checking off

To get checked off, show your results for the exercise to a CP or TA. This should include: