CSCI 103L - Fall 2024 Introduction to Programming

CS102 Spring 2021 Final - Within

In this program, the user will input 2 or more x,y points on a Cartesian plane and your task is to determine if at least one point is at most a distance/radius, r to ALL others (where r is a chosen and input by the user). Your program should:

1. First read in a distance threshold, r (assume r >= 0 ) from the keyboard which could contain a decimal.
2. Read in an integer n (assume 2 <= n <= 100 ) from the keyboard
3. Proceed to read in n pairs of numbers (could be decimals) representing the x and y coordinates of a point on the Cartesian plane ( the x value is entered first followed by the y value and is separated by whitespace).
4. Then determine if there exists at least one x,y point that is at most a distance, r, to all the other points. - If such a point exists, output a message containing that x,y point. (If many such points exists, you can output ANY single one of them…your choice which one). - If no such point exists, output a message indicating that.

You should store each x value in an array of x-coordinates and y value in an array of y-coordinates. Once entered, your code should check if at least 1 of the points has a distance of r or less to all others. Recall that the formula for the distance between two points: (x0,y0) and (x1,y1) is:

Note: It may be helpful to write a function to compute the distance between two points: double dist(double x0, double y0, double x1, double y1);

Example 1

For example, consider the example below with r=2.1 and 3 points: (-2,-1), (0,5), and (3,1):

2.1  3 
-2  -1
0  5
3  1

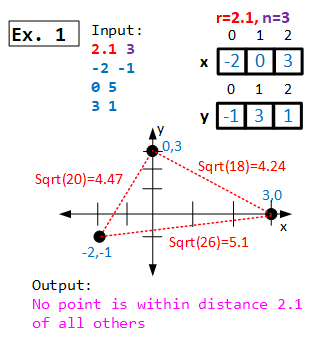
Because there is no point within distance, r=2.1, of all others, the program would output:

No point is within distance 2.1 of all others

Example 2

However, given the next example:

1.25  4
0  0 
1  0 
2  0 
1  -1 

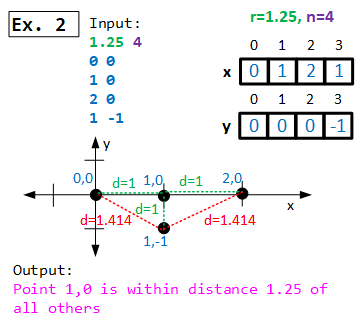
Only point (1,0) is within 1.25 of all others (it is a distance of exactly 1 to all three other points). The output should indicate success and list the point.

Point 1,0 is within distance 1.25 of all others

Example 3

If we assume the same inputs as Example 2 (above) but now r is entered as 1.5 (as shown below), then point (1,0) and (1,-1) are within a distance of 1.5 of all others. You could choose which one to output:

Point 1,0 is within distance 1.5 of all others

or

Point 1,-1 is within distance 1.5 of all others

Requirements & Assumptions

• The input representing n (number of points) is guaranteed to be 2 or more.
• The input representing r will be positive.
• Inputs can be doubles and not just ints.
• Any output of a double can be printed with arbitrary precision (you don’t need a fixed number of decimal places for your outputs).
• You can output any point that satisfies the criteria. You need NOT find ALL points that satisfy the criteria.
• Your output message should be the appropriate message from the two shown below, where r is replaced with the actual distance input by the user, and x,y is replaced with the satisfying x,y coordinate values (as shown in the examples above).

Point x,y is within distance r of all others

or

No point is within distance r of all others

The skeleton file can be downloaded with the link: within.cpp.

(You may need to right-click and choose Save As or Save Target As to download the .cpp file or open it in your browser and save the file.).