1 - Binary Trees
What does it mean for a tree to be binary?
A tree whose elements have at most 2 children is called a binary tree.
A Binary “Search” Tree (BST) is a specific type of binary tree. In a BST, left children (the left subtree) hold values that are less than the parent’s value, and right children (the right subtree) hold values greater than the parent’s value.
2 - Traversals
A traversal is a methodology for stepping through a structure (such as using Breadth-First Traversal as opposed to Depth-First Traversal on a graph). BFS is sometimes called “Level-Order Traversal”. In the base of DFS, there are a few different ways we can traverse.
The three main DFS traversals are Pre-Order, In-Order, and Post-Order . In each of these traversals, we must eventually operate on every node, they’re just being operated on in a different order.
Pre-Order Traversal
// Operate on current node
// Recurse left
// Recurse right
// return
In-Order Traversal
// Recurse left
// Operate on current node
// Recurse right
// return
Post-Order Traversal
// Recurse left
// Recurse right
// Operate on current node
// return
Fun questions
- For a BST, what is special about operating on elements using an in-order traversal? If we were printing integers using this traversal, what would the output look like?
- If we wanted to delete an entire tree without having to do much work, which traversal would we use?
- What is the third kind of DFS traversal? When would it be useful?
3 - Searching
BSTs exist to enable (potentially) fast searches.
Why do we say potentially? Can someone think of an example in which the search is really slow, even if we have a valid BST?
Our search function will simply return true or false depending on whether or not our search parameter exists in the tree. Another reasonable return value of a search function could be an iterator pointing to the found element (see std::map find).
To search for key X in a BST, we compare X to the current node.
- If the current node is null,
Xmust not reside in the tree. - If
Xis equal to the current node, simply return the current node. - If it is less than the current node, we check the left subtree.
- Else, it must be greater than the current node, so we check the right subtree.
3.1 - Example
Take a look at this example:
Operation: find(6)
Let’s walk through this.
Operation: find(6) // We begin at the Root
Current node is 8
is 6 == 8? No, go left (since 6 < 8)
Current node is 3
is 6 == 3? No, go right (since 6 > 3)
Current node is 6
is 6 == 6? Yes, return true
Now, here’s an example where we try to find a node that does not exist in the tree:
Operation: find(0)
Let’s walk through this one too.
Operation: find(0) // We begin at the Root
Current node is 8
is 0 == 8? No, go left (since 0 < 8)
Current node is 3
is 0 == 3? No, go left (since 0 < 3)
Current node is 1
is 0 == 1? No, go left (since 0 < 1)
Current node is empty
return false
The best-case runtime for searching a value X in a BST with N elements is O(logN).
### Fun questions
- What is the worst-case runtime?
- What does the tree look like for such a case?
- What is required to enable
O(logN)time searches in a BST?
4 - What’s a balanced Binary Search Tree?
Most operations on a BST take time directly proportional to the height of the tree, so we want to keep the height small.
A balanced BST is a tree that automatically keeps its height small (guaranteed to be logarithmic) for a sequence of insertions and deletions. This structure provide efficient implementations for abstract data structures.
A tree is considered balanced if it conforms to the Height-Balancing property. A node in a tree is height-balanced if the heights of its subtrees differ by no more than 1.
Here is an example of balanced vs. non balanced trees.
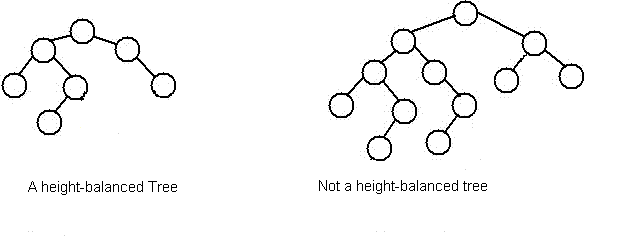
How can we maintain these properties?
The BST property is maintained by smart insertion and deletion. In an insert, you traverse the tree based on the key to be inserted. Once you encounter a situation where you can’t traverse any further, you know that the key can be placed there. Because we are traversing based on the key value, we are inherently upholding the BST property.
The same thing can be said about a deletion. This is done by choosing which node to promote. Either the predecessor, if the node has two children, or the child if the node has 1 child. By doing this, the BST property is being maintained.
A BST that maintains its balance throughout all insertions and deletions is called a self-balancing BST. These types of trees that auto-balance or self balance inherently with the insertion are called Self-Balancing Binary Search Trees. Examples are:
- Splay Trees
- AVL Trees
- Red Black Trees
- B-Trees
- 2-3 Trees
For all of these trees, the height-balancing property is upheld by the nature of an insert or remove. The best way to do so is with rotation, or series of rotations.
AVL Trees
An AVL tree is a type of balanced Binary Search Tree that uses the height of substrees and rotations to maintain balance.
Rotations
A rotation changes the local structure of a binary tree without changing its ordering. This means that in between rotations, the BST property is still maintained.
Rotations can be broken up into left and right rotations which are just inversions of eachother.
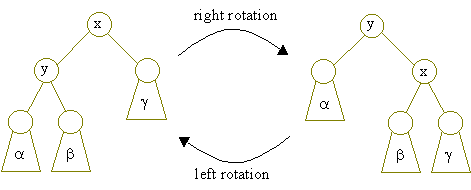
Rotaions make up the foundation of the AVL tree. You will eventually need to implement these rotations in a variety of scenarios in your homework. There are 4 combinations of rotations: left-left, left-right, right-left, right-right. Sometimes, these rotations are referred to as “zig zig” or “zig zag”, or something similar. The point is, during these sequences of rotations, the tree becomes more balanced than it was before.
If longer subtrees are left and then left
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
If longer subtrees are left and then right
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
If longer subtrees are right and then right
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
If longer subtrees are right and then left
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
By using combinations of rotations during insertion and removal, we are able to maintain consistent balance throughout the lifetime of the tree.
Inserting
- We start by inserting the value at its correct location as a normal BST would.
-
We traverse up the tree, evaluating the local height of each node and fixing that portion if the height of the left and right subtrees differ by more than 1 or less than -1.
Note:
- We only need to traverse up the tree from the inserted node because the subtree containing the new node is the only subtree where height can change and we need to rotate.
- We fix the tree beginning with the newly inserted node.
Removing
- We remove as normal and then proceed to fix the tree by traversing up, starting with the parent of the deleted node.
-
In the case that we are swapping with the predecessor, you continue to delete the same node until you cannot swap any further, and then begin fixing the tree in the same fashion.
Note: We fix the tree beginning with the parent of the deleted node.
Lab Activites
There are 3 activities you need to submit/show a TA/CP to get checked-off for this lab. The last activity is optional.
1. Simple Traversal
Given this binary tree:
What order will the nodes be printed out with 1) Pre-Order traversal? 2) In-Order? 3) Post-Order?
- Answer the above question and save your answers in a file name
lab8.txt
Next, you’ll have to complete these two binary tree traversal problems:
A node is defined as such (see bst.h):
class Node {
Node *left;
Node *right;
int key;
}
2. Range sum
Given the root of a BST and two values L and R, return the sum of all the nodes in the tree with values between L and R (inclusive).
For example, If called on the tree in #1 with L = 1 and R = 6, the function should return 14 (1+3+4+6).
- Implement
rangeSuminbst.cpp3. Balanced tree
Given a binary tree, determine if it obeys the height-balancing property.
For this problem, a height-balanced binary tree is defined as:
- a binary tree in which the height of the two subtrees of every node never differs by more than 1.
Hint: A helper function that determines the height of a tree given the root node may be useful.
bool isBalanced(Node *root)
- Implement
isBalancedinbst.cpp
4. AVL Insertion and Deletion (Optional)
Take some time to confirm your understanding by showing the tree after each of the following operations. You can ask the CP/TA to confirm your answer.
Initial Tree
13
+--------+--------+
10 15
+---+---+ +---+
5 11 16
+---+---+
4 8
- Insert 14
- Insert 3
- Remove 3
-
Remove 4
- Show what the tree looks like after each of the above operations. Operations should happen sequentially (i.e., Insert 3 happens after Insert 14).
Check off
Submit appropriate screenshots or files at this form. If you are in the synchronous lab and show your work to a TA/CP, you do not have to submit to the form.
Use make to run the test cases for rangeSum and isBalanced.
Show a TA/CP you passed tests.
Show a TA/CP your answers for #1.
If you use the form,
- Submit your
lab8.txtcontaining answers to #1. - Submit screenshot of your
bst.cppfile. - Submit screenshot(s) of all tests passing for both functions (
rangeSumandisBalanced).

