Heaps & Priority Queues
In today’s lab, we’re going to focus on priority queues, an important data structure that you’ll need to understand for this course.
Introduction to Heaps
In office hours, we usually have a queue where the student who came in the earliest is called next. This is the standard FIFO (First-In-First-Out) queue.
But what if we wanted to apply a more complicated calculation to found who was next? Maybe the person with the shortest question? The person who started the assignment the earliest? The person who’s asked the fewest questions? We still want the popping functionality of a queue, where we can easily determine who’s next, and don’t need to call on anyone in the middle. However, we no longer want to process items in order of arrival (i.e. First-In) – instead we define our own function for assigning the priority of elements in the queue.
Q: How do we add, return, and remove items based on their assigned priority?
A: Use a priority queue. It allows us to add items to their appropriate location based on their priority, and get the item of highest priority. Heaps are an implementation of a priority queue.
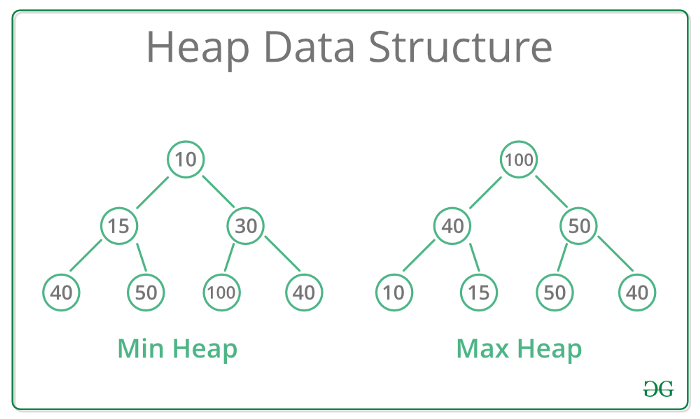
You can visualize a heap as a complete d-ary tree (usually, d = 2) that satisfies the heap property:
Every parent is ‘better’ than its children.
In a min heap, it means a node is less than or equal to all its children. In a max heap, it means a node is greater than or equal to all its children.
-
So, where in the tree is the “best” (maximum or minimum) item at any given time?
-
For a binary heap, does it matter which child is on the left and which child is on the right? Why or why not?
-
In what data structure is there an ordering property between the left and right children, and why is it necessary for that data structure and not in heaps?
Storage of heaps
Since a complete tree is one where the first (h-1) levels are full AND the bottom level is filled from left to right, we can store our heaps in a single array.
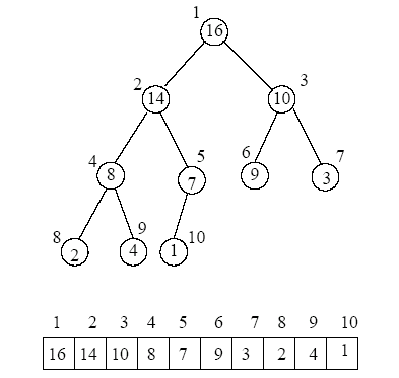
Suppose we index our array starting at index 1. For any node i, parent(i) = i/2. For any parent p, left_child(p) = 2p and right_child(p) = 2p + 1.
- How does this change if we index our array starting at index 0?
If we start at index 0, for any node i, parent(i) = (i - 1)/2. For any parent p, left_child(p) = 2p + 1 and right_child(p) = 2p + 2.
- How does that change if we have a 3-ary heap, 4-ary heap, 5-ary heap, etc.?
That’s for you to figure out in the homework!
Thankfully, implementing the functions of a priority queue is not as hard as it sounds. Let’s say our heap is stored in an array a, and the variable size returns the number of items in the heap at a given time.
Pushing an Item: to add an item, we need to think about where to add it. In what location should we add our new item if we want to keep our tree complete? What index of our array does this correspond to? Adding the item is the easy part; after adding, we need to think about maintaining the heap property as well. If our newly added leaf is worse than its parent, does our heap property still hold? This is where “trickling up” comes in: to maintain the heap property, we need to recursively promote our new leaf up. How do we know when to stop “trickling up?”
Popping an Item: recall that when we remove from a heap, we are removing the best item. However, the best item is stored in the root, and we can’t just delete our root from the tree! In fact, the only item we can remove while maintaining a complete tree is the leaf node that is as far right as possible. Removing an item is going to involve three main steps:
a. Swap the “best” node with the very last leaf node. Where are these stored in our array?
b. Delete the very last leaf node (which now stores our “best” item.)
c. Since the root now contains what was previously our very last leaf node, we are going to have to put it in its right place to maintain our heap property. The last step of removing involves “trickling down”: recursively swapping our new root with its best child. How do we know when to stop “trickling down?”
Top/Returning Best Value: to return the best value, all we have to do is return a[0]. The runtime of top() is clearly constant. What are the runtimes of adding/removing an item? (Hint: what is the height of a complete d-ary tree?)
Assignment
There’s no starter code for this lab, but you can create your own .cpp file for the exercise.
ROCK BATTLE:
We have a collection of stones. Each stone has a positive integer weight. The stones are represented as a vector of ints, where each int is the stone’s weight.
We want our rocks to battle. Each turn, we choose the two heaviest rocks and smash them together. Suppose the stones have weights x and y, where x <= y. The result of the smash is:
If x == y, both stones are totally destroyed.
If x != y, the stone of weight x is totally destroyed, and the stone of weight y now has weight y-x.
At the end, there is at most 1 stone left. Return the weight of this stone (or 0 if there are no stones left.)
You’re encouraged to use vectors as well as the STL heap (specifically make_heap, push_heap, and pop_heap) or priority queue.
Note: this algorithm-based problem is similar to what you might see in CSCI 270!
Lab Submission
Submit appropriate screenshots or files at this form. If you are in the synchronous lab and show your work to a TA/CP, you do not have to submit to the form.
What to submit:
- screenshot of your implementation of the function
int lastStoneWeight(vector<int> &stones)that solves the Rock Battle problem

