***
←
→
Topics
Function structure
Function examples
Recursion
Overloaded functions
Inline functions
Default values for inputs
Structure, purpose
In every programming language, functions serve two purposes:
* they help ABSTRACT away code
* they help REUSE code
Functions are also called routines, subroutines, procedures, methods etc. Regardless of what they are called, they are INVALUABLE! Programming simply can't exist without them.
Abstractly speaking, this is a function:

A function can optionally have INPUTS, and can optionally have an OUTPUT too.
Let us now examine four variations (the only possible ones!) of a function:
* a. no inputs, no output
* b. has inputs, no output
* c. no inputs, has output
* d. has inputs, has output
Function: a. no inputs, no output
Here is an example of defining and calling a function that has no inputs, no output (not very useful!):
#include <iostream>
using namespace std;
// DEFINE/CREATE function
void printTemperature() {
cout << "It is 70 degrees F!" << endl;
}// printTemperature()
int main() {
// CALL/RUN/EXECUTE/USE/INVOKE function
printTemperature();
return 0;
}// main()
As you can see from the above, when called, the function runs, and produces a cout - but we have no way to control/influence/modify what the function does (eg. we can't make it print 85, for example).
Function: b. has inputs, no output
The following function accepts/requires two inputs from the user.
#include < iostream>
using namespace std;
void add2Nums(int a, int b) {
int sum = a+b;
cout << sum << endl;
}// add2Nums()
int main() {
// CALL/RUN/EXECUTE/USE function
add2Nums(4,8);
add2Nums(34,-35);
return 0;
}// main()
Note that printing (via cout) is NOT considered output! So the above function takes two inputs, but produces no output.
srand(seed) is a real-world example of a function that takes an input (seed value) but returns nothing.
Function: c. no inputs, has output
#include <iostream>
using namespace std;
#include <cmath> // M_PI is defined here
double piOverTwo() {
return 0.5*M_PI;
}// piOverTwo()
int main() {
// CALL/RUN/EXECUTE/USE function
double p = piOverTwo();
cout << p << endl;
cout << piOverTwo() << endl;
cout.precision(15);
cout << fixed << M_PI << endl;
return 0;
}// main()
In the above, the function called piOverTwo **always** returns the same result.. This is not very useful.
Function: d. has inputs, has output
#include <iostream>
using namespace std;
#include <cmath>
double hypot(double base, double height) {
double h = sqrt(base*base + height*height);
return h;
}// hypot()
int main() {
double hypoten = hypot(3,4);
cout << hypoten << endl;
return 0;
}// main()
Functions with BOTH inputs **and** output (such as hypot() above) are the most useful kind! Think of these as 'chips' (ICs) that have input pins, and an output.
Functions: notes
* a function definition/declaration looks like: **returntype funcname (input) {body}**
* after giving the code body a name (after defining a function), we can USE (call/execute/run) the code body by simply specifying its (function) name [and any required inputs]
* a function that accepts inputs does so via '( )'
* when calling, the inputs' "signature" (what type, in what sequence) MUST match the signature in the declaration
* a function that outputs a value MUST do so via 'return' statements
* a function can only output a SINGLE result!
Functions: return value
A function's return value is a BIG deal! The return value is what MAKES A FUNCTION "TURN INTO" A VALUE, just like an expression such as 4.5*2/3.0, or a variable 'i' (eg. with int i=4).
That is why a function call's output can be used in an expression, and/or stored in a variable! Eg.
double twiceHyp = 2.0*hypot(5.6,7.8); // used in an expression
double h = hypot(1.0,3.56); // stored in a var
To repeat, the execution of a function that has a return (output), "turns into", or "stands for", its output; in that sense, it is somewhat like a variable (which "returns" its value when we "read" [access] it).
And, a function that takes inputs and returns a computed value (aka "computes a return value"), eg. sqrt(9), is analogous to a FORMULA that takes variables, and computes a return value.
Call chaining/cascading
A function's inputs can come from other functions:
double h1 = hypot(1,2);
double h2 = hypot(3,4);
double h3 = hypot(h1,h2);
// why even use variables h1 and h2 - no need!
double h = hypot( hypot(1,2), hypot(3,4) ); // identical to h3 above
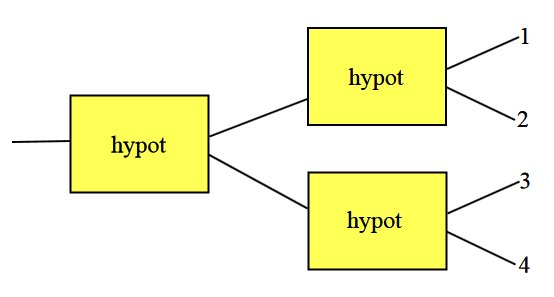
Function definitions can use other (existing) functions
A BIG IDEA in programming, is this: inside a function definition, we can call (make use of) previously defined functions! This way, we can build ladders of abstractions. Note that such previously defined functions can even be 'library' (pre-written) functions.
Eg. given 'double add2Nums(double a, double b)', how can we create 'double add4Nums(double a, double b, double c, double d)'?
add4Nums, given add2Nums
The following illustrates the 'BIG' idea of calling a function, INSIDE the definition of another function:
#include <iostream>
using namespace std;
double add2Nums(double a, double b) {
return (a+b);
}// add2Nums()
// make use of add2Nums THREE times!
double add4Nums(double a, double b, double c, double d) {
// we're using the 'big idea' of calling an existing
// function (add2Nums()) three times, inside the body of
// (ie. while defining) add4Nums
double sum1 = add2Nums(a,b); // partial sum
double sum2 = add2Nums(c,d); // another partial sum
double total = add2Nums(sum1,sum2);
return total;
}// add4Nums()
int main() {
double t = add4Nums(1,2,3,4);
cout << t << endl;
return 0;
}// main()
Exercise: Rewrite add4Nums to contain just a single line (in the body).
Recursion (an 'elegant' idea in CS)
A function can call **itself** [in its definition]!
Many problems (eg. listing all the contents of a directory) can naturally be solved using recursion (likewise for sorting, etc.).
Recursion looks like this:
n! = n*(n-1)!
0! = 1
Computing the factorial of n can be coded like so [uses recursion]:
#include <iostream>
using namespace std;
int factorial(int n) {
if(n==0)
return 1; // bottom out!
else
return n*factorial(n-1); // recurse!
}// factorial()
int main() {
int nFact = factorial(10);
cout << nFact << endl;
return 0;
}// main()
Check the result: https://www.wolframalpha.com/input/?i=what+is+10!
Exercise: create a different 'int factorial(int n)', one that does NOT use recursion.
Note - there is MUCH more to recursion, than using it to compute factorials! Practically every algorithm that deals with a graph or tree (two 'workhorse' data structures in computing) is a recursive one.
One more small example: to sum up the elements of an array, here is an informal, recursive definition: arraySum = currentValue + arraySum-of-the-remainder-of-the-array. Exercise: turn this into code, using a recursive arraySum() function. Here is the solution.
Function overloading
Earlier, we saw that the / operator is overloaded (can perform integer division, or floating point division).
Likewise, we can have function overloading, where a function (eg. myFunc()) can have MULTIPLE (different) signatures. Note: this is a very useful, "C++ only" feature, is NOT available in C.
Eg. let us create an average() function that takes 2 inputs and averages them 50/50 (calculates the mean), AND an average() function that takes 3 inputs, where the first input is a weighting factor for the other two.
Example: average() - overloaded function:
#include <iostream>
using namespace std;
// 2 input version
double average(double x, double y) {
return 0.5*(x+y);
}// average()
// 3 input version
double average(double wt, double a, double b) {
return wt*a + (1-wt)*b;
}// average()
int main() {
double a = average(4,5);
cout << a << endl;
a = average(0.5,4,5); // same as average(4,5)
cout << a << endl;
a = average(0.2,4,5);
cout << a << endl;
return 0;
}// main()
Exercise: simplify the second definition (3 input version) of average() [also, why bother?].
Note that overloading CANNOT be used with differing return types, eg. a function x() that returns an int, and another function, also named x(), that returns a double; overloading can only be used to define identically-named functions that have differing input signatures.
inline functions
Sometimes, for a small function that you're going to use just a few times, it would help 'inline' the function definition - when the compiler sees such an inline definition, it will REPLACE the function call with the inlined code, thereby saving a function call (which will speed up processing).
inline int squared(int a) {
return a*a;
}// squared()
int x=4;
int y = squared(x);
// the above call would actually become
// int y = x*x;
// before getting compiled.
Default function arguments
You can provide default values, ie. "factory settings", for a function's inputs so that the callers of the function can omit providing those inputs. Here is an example:
#include <iostream>
#include <cmath>
using namespace std;
// declare a function *prototype*, with default value(s):
// a prototype names a function's signature, without providing
// the body (which comes later - can even come AFTER [following] the
// function's calls)
double mySqrt(double x=4.0); // if 'x' is left out, use 4 as its value
int main()
{
cout << mySqrt(5) << " " << mySqrt() << endl;
return 0;
}// main()
// function body, for the prototype declared earlier
double mySqrt(double x) {
return sqrt(x);
}//mySqrt()
Here is another example, where we don't declare prototypes but do provide defaults for args. The logX() function is useful in practice, where you can omit the logarithm base, to have the default of 10 be used:
#include <iostream>
#include <cmath>
using namespace std;
// logX returns the log of a number for an arbitrary
// base (which, if omitted, defaults to 10)
double logX (double y=10, double base=10) {
return (log(y) / log(base));
}// logX()
double hy(double a=3, double b=4){
return sqrt(a*a+b*b);
}// hy()
int main()
{
cout << logX() << " " << logX(1000) << " " << logX(1000,2.7) << endl;
cout << hy() << endl;
return 0;
}// main()
Why use function prototypes?
In an earlier example, we declared a prototype for mySqrt (as shown below) and provided its implementation later [underneath main()].
double mySqrt(double x=4.0); // prototype
But what is the purpose of this, ie. why bother declaring prototypes?
One answer is that it is a "good habit", where we first create a set of function prototypes (and declare them at the top of our file), and start USING THE FUNCTIONS (calling them) **even before** we write the implementation! A prototype serves as an 'interface' that both callers AND the implementer must 'honor' (it is a "contract" between those two entities).
Another answer: prototypes are what make it possible for us to use every 'library' function in our code, including math fns, eg. sqrt()), OpenGL functions (for graphics), etc. The header files we #include (eg. #include < cmath>) contain prototype declarations, and the actual definitions are in separate library files (eg. opengl.dll, libm.a) THAT GET LINKED AFTER our own sources are compiled - without those #includes, we would get a 'function not declared' error if we try to use sqrt() etc. [try it!].

