CS455 Final Exam
6/24/21
Please note the following:
* submit your work on D2L, under the 'Exam' slot
* you can use ANY software you want - editors, IDEs, shells, compilers, viewers etc.
* you are allowed to look up ANYTHING ANWHERE - online, your own files, books, cheat sheets.. anything at all!
* you can't get anyone else's help with any part of any question; a LOT of trust is being placed on you to do the right thing, please honor it! It is NOT worth getting ahead using unethical means.
* please observe the time limit of ~2 hours [a 'bit' over is OK!]
There are two questions: a C++ one, with three parts; a Java one, also with three parts. So you need to allocate about 20 minutes for each of the 6 parts. In each question, the parts are labeled a,b,c.
Have fun! Hopefully it is a straightforward exam, and hope you enjoy thinking about and coding the solutions.
Q1. 3+4+3=10 points.
Random number generation and usage is a serious matter. But for our purposes, here is a nice little random number generator class called 'Rnd' that contains these members and methods:
members: last, seed, mpyer, adder, count. 'last' holds the last random value that was generated, seed is the usual seed (needs to be between 0.0 and 1.0), count is the # of values generated since the start, and mpyer and adder are internal (LCG) values that help carry out the generation
methods: Rnd() [two constructors], random() [returns a 0..1, double type, pseudorandom number value], getCount() [returns the 'count' var], and reset() [resets the count to 0, and sets 'last' to the very first value - in other words, it starts the generation and sequence all over again]
This is the entire 'Rnd' class discussed above:
class Rnd {
private:
double last=0.1; // latest # in our sequence
double seed=0.1; // a seed value, between 0.0 and 1.0
double mpyer=309.0, adder=0.203125; // for our LCG formula
int count=0; // how many nums served so far
public:
Rnd(double s){
seed = s;
last = s;
}// Rnd
Rnd(){
}// Rnd
double random() {
last = mpyer*last + adder;
last -= int(last); // same as last %= 1.0;
count++;
return last;
}// random
int getCount() {
return count;
}// getCount()
void reset() {
last = seed;
count = 0;
}// reset
};// class Rnd
Note that the random() method uses the classical LCG technique to generate values:
X_n = (aX_n-1 + c) mod m
Create a folder called Q1, and place Rnd.h inside it. Now create a main.cpp, which you'll use to code up the three items below. Here is a starter main.cpp for you:
#include < iostream> // remove the space between < and iostream
using namespace std;
int main() {
return 0;
}// main()
Note that we initialize and call Rnd this way (do this in your main.cpp and run it):
// Rnd rng(0.0055); // with a seed
Rnd rng; // without a seed (defaults to a seed of 0.1)
for(int i=0; i<100; i++)
{
cout << rng.random() << endl;
}
cout << "Count: " << rng.getCount() << endl; // 100
rng.reset(); // restarts the sequence!
for(int i=0; i<105; i++)
{
cout << rng.random() << endl; // the first 100 values will be identical to the previous set
}
cout << "Count: " << rng.getCount() << endl; // 105
You can see that using Rnd is very straightforward.
a. characterize the generator. In other words, run the generator 10,000 times, count how many values fall between 0..0.1, 0.1..0.2, etc. up to 0.9..1.0. To do so, create 10 bins, and increment the appropriate one for each new random() result. Output the 10 totals, below each other - we expect them all to be nearly identical, each nearly equal to 1000 (because our generator is hopefully an unbiased one and yields a uniform distribution). Just output the counts (totals), no need for printing out asterisks.
b. subclass Rnd to create a Die class. The Die class is for simulating the roll of a single Die - it will output 1,2,3,4,5 or 6 during each roll(). You can write the Die class inside main.cpp. Do this as part of writing Die (note that Rnd's reset(), getCount() and random() don't have to be modified here in Die):
* write Die(double s) which will accept a seed and call the parent with it; also write a Die(){}
* write a .roll() method that outputs a 1..6 int value. Note that you have access to (can call) random() because that comes from the superclass. So, transform random()'s output into a 1..6 int. Hint: note that the built-in int() function can create an int from a double (ie. can perform truncation), eg. int(12.543098) will be 12
Once you write Die, ie. do the above items, you can use it like so (do this in your main.cpp and run it):
Die d1(0.45),d2(0.3678);
for(int i=0; i<100; i++)
{
cout << "d1: " << d1.roll() << endl; // 1 through 6, 1/6 probability for each
}
cout << d1.getCount() << endl;
c. roll two dice multiple times, verify that their sum yields a binomial distribution. In other words, when you do d1.roll() and d2.roll() and sum them, you will get a sum between 2 (when each die produces a 1) and 12 (when you get 6,6). A total of 7 can happen six different ways: (1,6), (2,5), (3,4), (4,3), (5,2) or (6,1) - so there are more chances to get a 7, than to get a 2 or 12. In other words:

[from http://www.cs.cornell.edu/courses/cs280/2007sp/280wk10_x4.pdf]
Create an int array called counts[13] and fill it with 0s. We can use this to count how many 2s, 3s, 4s.. 12s we get (using elements [2],[3]..[12]).
Create two dice, d1 and d2 - be sure to INITIALIZE EACH WITH A *DIFFERENT* 0.0..1.0 SEED!! Loop 100,000 times roll d1, d2, sum their values if sum is 2, counts[2]++ .. if sum is 9, counts[9]++ .. Done looping
Rather than just print out the 11 totals (for 2,3,4,5..12), use the printStars() function below, which also prints the value from each counts[] at the end of each row of stars.
void printStars(int n, int value) {
for(int i=0;i < n;i++) {
cout << "*";
}
cout << " " << value; // the value is what the n stars represent
}/// printStars()
For each of the 11 totals, divide it by 100,000 and multiply by 100, truncate, to get a star count. As a point of reference, my output looks like this:
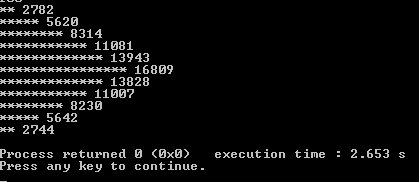
As you can see, we get a nice distribution as expected - most of our dice sums did indeed turn out to be 7.
Q2. 3+4+3=10 points.
a. implement the Rnd C++ class from Q1, in Java. Make a Q2 folder, inside it, create Rnd.java, 'port' the C++ class over (same members, methods). Create a psvm and use it to verify that your class works:
Rnd rng = new Rnd(); // default seed of 0.1 gets set
for(int i=0; i<100; i++)
{
System.out.println(rng.random());
}
System.out.println("Count: "+rng.getCount());
rng.reset();
for(int i=0; i<105; i++)
{
System.out.println(rng.random());
}
System.out.println("Count: "+rng.getCount());
Note that the random number sequence is identical to what we get from the C++ version of the class :) That is because we rely on our own code (using the multiplier, adder, and truncation or mod) for the generation.
b. estimate a value for pi, via 'dart throwing'. Consider the following figure - it shows a 2x2 square and an embedded radius=1 circle [origin (0,0) at the center of the figure].

A bad dart thrower would uniformly cover the region (square) with random dart locations. The RATIO of the # of darts that fall inside the circle to the total # of darts (tries) thrown, is a measure of pi! Such random-number-based estimation techniques are called Monte Carlo algorithms.
numThrowsInsideCircle/numThrowsTotal = area of circle/area of square = pi*r*r/(2*r*2*r) = pi/4
pi = 4.0*numThrowsInsideCircle/numThrowsTotal
int nThrows = 100000000;
int nInsideCircle=0;
start a random # generator (of type Rnd - the class you wrote!)
loop for nThrows:
x = -1..1 randomly
y = -1..1 randomly
IF the throw (x,y) lands inside the circle (of radius=1)
[if distance between 0,0 and x,y is less than 1],
increment nInsideCircle
next
pi = 4*....
print pi
Write, inside the Q2 folder, a calcPi.java program to do the above calculations in psvm.
c. create a Java program that will output a .wrl file containing a volume lattice (cubical xyz grid) of spheres, with a random radius (0..1) and random transparency for each sphere.
We want something like this:

Inside Q2, create a voxelGrid.java program, containing this class:
class voxelGrid{
int xRes=10, yRes=10, zRes=10;
double lattice[][][] = .. // a 3D array
Rnd rng = ..
Include a constructor so the user can specify xRes,yRes,zRes, eg.
voxelGrid v = new voxelGrid(25,25,25);
Create 'void fillLattice() {..}' - with a triple for() loop, fill the lattice [][][] array with random 0..1 values. We can think of each cell value as a 'density'/'transparency' value for the cell.
Create 'void outputWRL(String outFile)' that saves out the lattice data as a viewable .wrl file. Modify the .wrl example from class or lab, to place spheres at each x,y,z of the lattice. The radius of the sphere at a location [i,j,k] should equal the lattice[][][] value stored there; additionally, the material transparency should ALSO be equal to the stored lattice[][][] value (in other words, use each stored value to be the radius AND transparency). Use code such as this, for transparency:
out.println(" appearance Appearance {");
out.println(" material Material {" + "transparency " + rad + "}");
out.println(" }");
Again, you are systematically filling lattice[][][] with 0..1 random values, then looping through the lattice to place a sphere at each location, with the sphere's radius and transparency coming from the lattice[][][] value at the location.
To test, from the psvm in voxelGrid.java you can simply do:
..
voxelGrid vg = new voxelGrid(20,20,20);
vg.fillLattice();
try {
vg.outputWRL("C:\\temp\\test.wrl");
}
..
..