HW4
Please complete the coding exercise below, and as usual, submit your source code on D2L.
Q1. Class construction (25 points)
The task is to create a fractal program that:
* renders a color fractal to a screen window
* writes the (color) pixels to a .ppm image.
You need to implement the following three classes/sources:
* Mandelbrot: for the fractal calculation
* ComplexNumber: for representing a complex number, and doing ops (squared or multiplication, addition) on it
* ColorList: for creating a randomized color list (ArrayList<Color>) with 256 entries (that way, we can use a 0..255 fractal calc value as an index into here, to lookup a color; in other words, gray in, color out).
Here is how you can approach the problem:
Mandelbrot:
* members: xtable[][],xRes,yRes,cxMin,cxMax,cyMin,cyMax, colors (of type ColorList to hold java.awt.Color values)
* methods: Mandelbrot (constructor, with arguments so the user can pass in xRes,yRes,cxMin,cxMax,cyMin,cyMax) [eg. Mandelbrot mand = new Mandelbrot(640,480,-2,1,-1,1);], setPixel(Graphics g, int x, int y, int red, int grn, int blu) to set RGB of a single pixel, displayFractal(Graphics g) to render the fractal pixel-by-pixel on the screen, saveFractal(String fileName) to output the fractal as a .ppm image. In the constructor, fill the 'colors' ColorList object with colors so that they can be used for pixel display and for writing to disk.
ComplexNumber:
* members: real, imag
* methods: add, squared
ColorList:
* member (public): colList
* method: ColorList(): to fill up colList (of type ArrayList<Color>)
Have ColorList and ComplexNumber ready, then in Mandelbrot, do this:
* constructor: make 'colors' equal to 'new ColorList()', this will cause 'colors' to become filled with 'Color' type values; create xtable as a 2D array; fill up xtable using a double for() loop (do z <- z^2 +c [the usual Mandelbrot calculation], store a 0..255 'escape' value). At this point you'll have a grayscale version of the fractal ready.
* displayFractal: use the passed-in Graphics object 'g', and do setPixel() on it inside a double for() loop. For the RGB value to use, get() it from your 'colors' list, using the stored gray value (in xtable) as an index. What this means is the following. Earlier, you used, as a gray pixel value, s calculated iteration value (call it iter for example) for each pixel. Now, you would use iter as an array index, to pick a color (which is already calculated, because you'll create it before the double loop) that is stored in a ColorList object called 'colors'. So you would do colors.colList.get(iter) to get a Color value (call it c, for example). So now you can set pixel color r,g,b to be c.getRed(), c.getGreen(), c.getBlue(), rather than iter,iter,iter that you did before for the grayscale .pgm image. This is how we "convert" a scalar int value (iter) into a triplet (java.awt.Color) - by using the scalar int as a 'lookup' into a 'table' of colors (which is actually a linear list of colors). FYI, the color table in such a situation is usually referred to as a colormap or a 'LUT' (look up table).
* saveFractal: again, use xtable and colors to turn each pixel's gray value into an RGB triplet [do look up, ie. get()], then write out a .ppm image file (with a 'P3' header, and three 0..255 values for each pixel)
* psvm (main()): make a JFrame, JPanel, JLabel, BufferedImage, IconImage, hook them all up, then createGraphics() to get the Graphics object for rendering pixels into. After this, construct a new Mandelbrot(with initialization arguments) object. Call the object's displayFractal() [pass in Graphics object], and then its saveFractal(). 'Pack' the panel in, then set the frame to be visible (that is what will make the displaying happen).
The SinglePanel.java program provided as a link at the end of HW3 will be very helpful for doing the displaying of the fractal (ie. creating a JFrame, BufferedImage etc. as mentioned above) - compile and run it, and study it, then incorporate what you need from it into your own code. Note that you also need your completed ColorList.java from HW3, in order to be able to compile and run SinglePanel.java.
So, in terms of what should happen: when the program (Mandelbrot.class) is run, that should result in a colorful fractal being displayed, and a .ppm of it created on disk. Use Irfanview or a similar program to verify that the image is shown correctly [should match the JFrame display]. Here is a view of what the fractal might look like (your image would likely have different colors compared to this, which is fine):
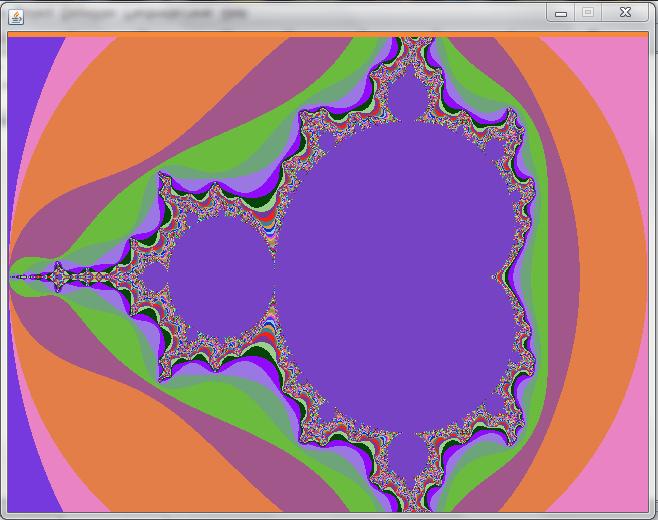
The above might seem overwhelming (hope not!), but there is not a single new concept, piece of syntax etc. that you need to learn in order to do this hw - everything you need you already have, in class notes' examples, homeworks, labs. This problem is simply meant to be an exercise in 'bringing it all together', where you make computations (eg. calculate the Mandelbrot set), display the result on screen as well as output it as a file - nice!
Please submit three source files: Mandelbrot.java, ComplexNumber.java, ColorList.java.
Note: on the Mac, drjava appears to have a display bug due to which the fractal display seems dark (black) almost everywhere (the .pgm image shows up fine). If this happens to you, don't be concerned, since we're aware of the problem.
Extra credit: Julia Set construction (3 points)
Create a 'Julia' class, similar to the Mandelbrot class - its purpose would be to compute and output Julia fractals (look it up - a Julia fractal is related to the Mandelbrot fractal). Overall, the Julia fractal calculation algorithm is identical to Mandelbrot's: z←z2+c. But here, we keep c constant, and instead, derive a different z for each (x,y) pixel location. Here is the algorithm psedocode (compare this to the Mandelbrot one from HW2):
create a blank image
set c = -0.7,0.27015 // fixed value, won't change for each pixel
set zMin, zMax to be (-1.5,-1) and (1.5,1)
for each y (in yRes)
for each x (in xRes)
x,y is our pixel coordinate. TRANSFORM this to a complex number 'z' as follows:
real = zxmin + x/(xRes-1)*(zxmax-zxmin) [maps x to zxmin..zxmax]
imag = zymin + y/(yRes-1)*(zymax-zymin) [maps y to zymin..zymax]
set z = (real,imag) // a different value at each pixel
set maxIter = 200
set iter=0
while (iter < maxIter and abs(z) < 2)
z = z^2 + c [iterate!!] [use .squared() and .add() from your ComplexNumber class]
iter++
end_while: either iter has exceeded maxIter, or abs(z) has exceeded 2
if abs(z)>=2 (we escaped our containing circle of radius 2!)
set index value to be iter
else (we got stuck, ie iter>maxIter but we're still inside the circle)
set index value to be 0
set pixel color to be ColorList[index]
write out image
Make a copy of your Mandelbrot.java source, rename it to Julia.java, modify the algorithm there to calculate Julia fractals as shown above. Include Julia.java in your .zip submission.
FYI below is an interactive program, written in JavaScript - click on any part of the Mandelbrot fractal shown, to see underneath, the Julia fractal at that clicked location: http://www.malinc.se/testinghtml5/juliaUsingHtml5.html. Also, look at this page: http://www.karlsims.com/julia.html
Good luck on this final homework :)
