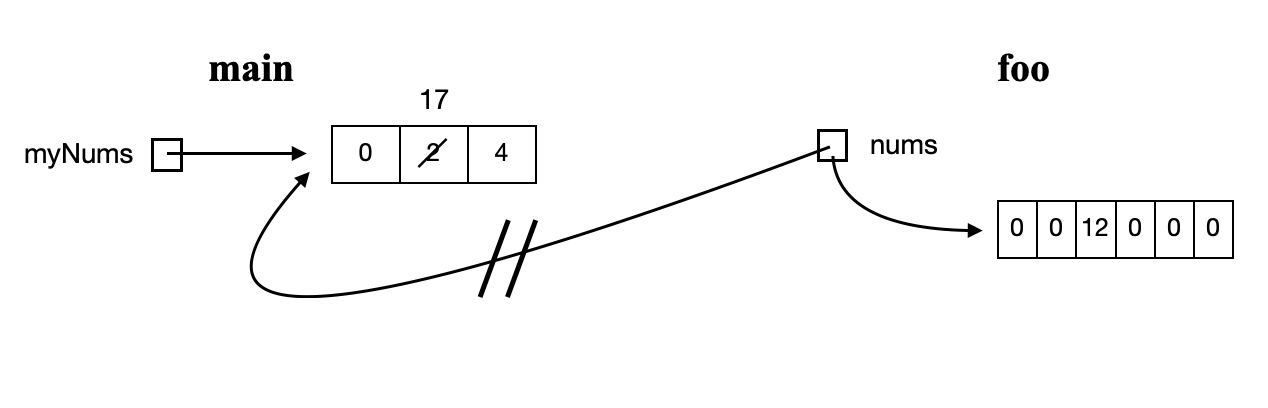
Part A.

Part B.
[0, 17, 4]
Problem 2
Part A. (Several correct solutions, here are a few)
Input = [5] Output = "5 + " Input = [5, 6] Output = "5 + 6 + "
public static String makeAdditionExpression(int[] nums) {
String expr = "";
if (nums.length == 0) { return expr; } // to avoid statement after the loop
for (int i = 0; i < nums.length - 1; i++) {
expr = expr + nums[i] + " + ";
}
expr += nums[nums.length - 1];
return expr;
}
public class FibonacciGenerator {
private int last;
private int secondLast;
public FibonacciGenerator() {
last = 1;
secondLast = -1; // special value to indicate first time we are calling next
}
public int next() {
if (secondLast == -1) {
secondLast = 0;
return 1;
}
int curr = last + secondLast;
secondLast = last;
last = curr;
return curr;
}
}
Problem 4
Part A. vals.size() = numVals
Part B. private ArrayList<Integer> vals;
Part C. (Any of the following accepted)
-Less code to write in the methods
-Less code to maintain
-Less error-prone, or illustrations of this, e.g.:
*Don't have to worry about updating numVals in mutators (or in add)
*Or give a scenario about adding new mutators later and forgetting to update numVals along with vals.
-Empty nums -Nums with one value -Minimum is somewhere in the middle of the ArrayList, and ArrayList size > 2 -Minimum is the first value in the ArrayList -Minimum is the last value in the ArrayList -Nums with multiple copies of the minimum value -Nums with all values as the minimum -Nums with only Integer.MAX_VALUE -Minimum is negative and ArrayList size > 1 -Nums with Integer.MIN_VALUE
public static ArrayList<Double> zeroCrossings(int[] nums) {
ArrayList<Double> result = new ArrayList<>();
for (int i = 0; i < nums.length-1; i++) {
if (nums[i] == 0) { // safe to access at i-1 because no 0s at the ends
if (nums[i-1] < 0 && nums[i+1] > 0 || (nums[i-1] > 0 && nums[i+1] < 0)) {
result.add((double)i);
}
}
else if (nums[i] > 0 && nums[i+1] < 0 || nums[i] < 0 && nums[i+1] > 0) {
result.add(i + 0.5);
}
}
return result;
}