Part A.

A note on the grading of Part A: To get full credit for a box-and-pointer diagram problem, you have to demonstrate that you know the differences between how primitive types and array types are handled in memory. Solutions that show primitive variables as references to memory locations (i.e., shown with an arrow pointing to a memory location) or show array variables as named blocks of memory, instead of references, do not receive full credit.
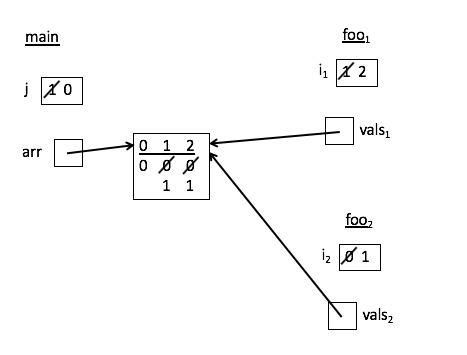
Part B.
2 [0, 0, 1] 1 [0, 0, 1] 1 [0, 1, 1] 0 [0, 1, 1]
Problem 2
Part A. Note: any valid input sequence will exhibit the bug;
here's one example.
input: 2 3 -1
return value: [2, 3, -1]
Part B. Here are two common correct solutions. (Changes shown in bold)
Solution 1:
public static ArrayListreadScores(Scanner in) { ArrayList<Integer> nums = new ArrayList<Integer>(); int score = 0; score = in.nextInt(); while (score != -1) { score = in.nextInt();nums.add(score); score = in.nextInt(); } return nums; }
public static ArrayListProblem 3readScores(Scanner in) { ArrayList<Integer> nums = new ArrayList<Integer>(); int score = 0; score = in.nextInt(); while (score != -1) { if (score != -1) { score = in.nextInt(); } nums.add(score); } return nums; }
Part A. Solution shown in bold.
/**
Duration represents some amount of time in hours and minutes.
*/
public class Duration {
// Problem restriction:
// do not change the private instance variable definitions
private int totMinutes; // representation invariant: totMinutes >= 0
/**
Creates duration of the given hours and minutes
PRE: hours >=0 and minutes >= 0
*/
public Duration (int hours, int minutes) {
totMinutes = 0;
increase(hours, minutes); // ALT version: repeat the formula here
}
/**
Creates a duration given as a total number of minutes.
PRE: totalMinutes >= 0
*/
public Duration (int totalMinutes) {
totMinutes = totalMinutes;
}
/**
Increase the current duration by the amount of time
given by hours and minutes.
PRE: hours >=0 and minutes >= 0
*/
public void increase(int hours, int minutes) {
totMinutes += hours * 60 + minutes;
}
/**
Returns the sum of this duration and duration "b"
This duration is unchanged by add.
Note the return type is a Duration object.
HINT: Java rules allow this method to access private data of other
Duration objects besides "this": for example, b's private data.
*/
public Duration add(Duration b) {
return new Duration(totMinutes + b.totMinutes);
}
/**
Returns a String form of the duration using the format shown by
example here: "8hrs 32min"
*/
public String toString() {
int hours = totMinutes / 60;
int minutes = totMinutes % 60;
return hours + "hrs " + minutes + "min";
}
}
Part B. No, duration objects are not immutable. The increase method changes the state of the object.
Problem 4
D. unknown
Why it's D: Part of the idea of encapsulation (aka, information hiding) is that the interface and the implementation of a class are independent from each other. E.g., you could have a Duration constructor that takes hours and minutes as parameters, and even have accessors, getHours and getMinutes in the same class, but that doesn't mean it necessarily has hours and minutes instance variables -- could be the representation we used on this exam instead.
Problem 5
There are several solutions. Here are two:
Solution 1: do it from the home directory:
mkdir $ASNLIB/public/02-07 cp * $ASNLIB/public/02-07Solution 2: change to the other directory
cd $ASNLIB/public mkdir 02-07 cp ~/* 02-07 (alternate to third command: cd 02-07 then cp ~/* . )
Problem 6
public static int mode(int[] nums) {
int[] counts = new int[101]; // count frequencies
for (int i = 0; i < nums.length; i++) {
counts[nums[i]]++;
}
// find smallest value that has max frequency
int mode = 0; // or -1
int modeFreq = 0; // ALT: don't save modeFreq (see other ALT comments)
for (int val = 0; val < counts.length; val++) {
// ">" here means we'll keep the smallest value that is also the mode
if (counts[val] > modeFreq) { // ALT counts[val] > counts[mode]
mode = val;
modeFreq = counts[val]; // ALT: eliminate
}
}
return mode;
}
The main alternate approach students used traverses the array
many times, finding the number of instances of nums[0], and then the
number of instances of nums[1], etc. in lieu of computing all the
counts into an array. That was not a full-credit solution, because
the problem specified to traverse the nums array only once for full
credit. An uncommon solution, but even more efficient than the one shown, is one that finds the mode in the same loop that computes the counts (still needs counts array). That version needs special-case code for tie-breaking (i.e., when counts[val] == counts[mode]), since we aren't visiting values in increasing order.