CS 455 Midterm 1 Solution

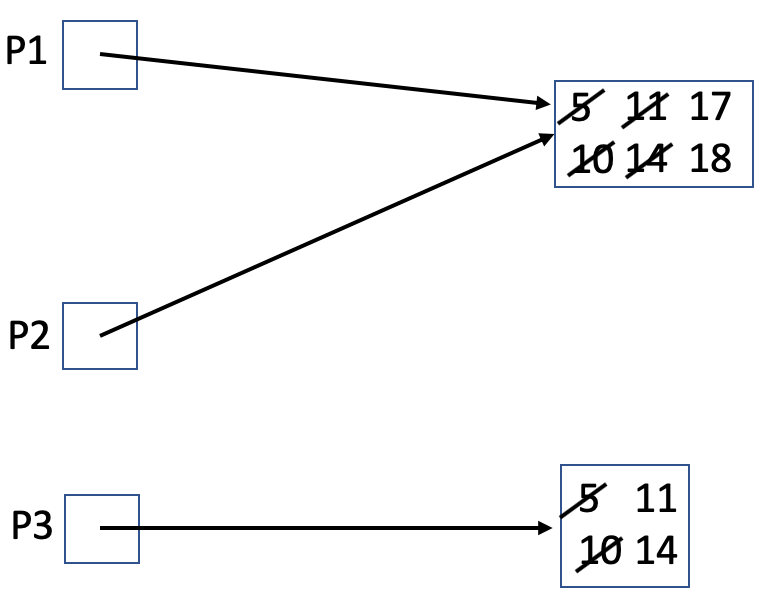
Part A.

A note on the grading of Part A: To get full credit for a box-and-pointer diagram problem, you have to demonstrate that you know the differences between how primitive types and object types are handled in memory. Solutions that show primitive variables as references to memory locations (i.e., shown with an arrow pointing to a memory location) or object variables as named blocks of memory, instead of references, do not receive full credit.

Part B.

Hoo-yah!
[17, 18] [17, 18] [11, 14] 

Problem 2 Many correct solutions.
Part 1. (wrong)

temp: 95
return value: cool

Part 2. (right)

temp: 59
return value: cold

Problem 3 java Foo < inData > outData

Problem 4 Solution shown in bold.

/**
   Simulates trials of repeatedly tossing two coins and allows the user to
   access the cumulative results.
*/
public class CoinTossSimulator {
   
   private Random random;
   private int numCoins;
   private int numTrials;  // optional: alternate solution computes value
                           // for getNumTrials by summing values in results array 
   private int[] results;

   private int NUM_SIDES = 2;  // constants not required to get full credit
   

   /**
      Creates a simulator to work with numCoins coins (no trials done yet)
      PRE: numCoins > 0 
   */
   public CoinTossSimulator (int numCoins) {
      
      random = new Random();
      this.numCoins = numCoins;
      numTrials = 0;
      results = new int[numCoins + 1];
      
   }

   /**
      Get number of coins used in the simulation.
   */
   public int numCoins() {
      
      return numCoins;
      
   }

   /**
      Get number of trials performed since creating the object.
   */
   public int getNumTrials() {
      
      return numTrials;
      
   }

   /**
      Get number of trials that came out with the given number of heads
      since creating the object. (In these trials the result was 
      numHeads heads, and (numCoins() – numHeads) tails.)
	PRE: 0 <= numHeads <= numCoins()
   */
   public int getResultsWith(int numHeads) {    
      
      return results[numHeads];
      
   }

   /**
      Runs the simulation for numTrials more trials. Multiple calls to this
	 method *add* these trials to the current simulation.  
      PRE: numTrials > 0
   */
   public void run(int numTrials) {
       
      for (int i = 0; i < numTrials; i++) {
         int numHeads = doOneTrial();       // using a helper method not required
         results[numHeads]++;
      }

      this.numTrials += numTrials;  // keep track of total since creation

   }

   // does one trial of tossing numCoins coins,
   // and returns the number of heads that came up 
   private int doOneTrial() {

      // code assumes a 1 means heads, and a 0 means tails
      int numHeads = 0;
      for (int i = 0; i < numCoins; i++) {
         numHeads += random.nextInt(NUM_SIDES);  // toss one coin
      }
      return numHeads;
      
   }

}

Problem 5

1. B
2. both
3. S
4. S
5. B (also accepted none, in case student interpreted as compile-error message)
6. B
7. both
8. S
9. none
10. S
11. B
12. both
13. B

Problem 6

public static boolean isLine(int[] vals) {
      
   if (vals.length < 2) { return false; }
      
   int slope = vals[1] - vals[0];
      
   for (int x = 2; x < vals.length; x++) {
      if (vals[x] - vals[x-1] != slope) { return false; }
   }
   return true;
    
 }

public static boolean isLine(int[] vals) {
      
   if (vals.length < 2) { return false; }
      
   for (int x = 2; x < vals.length; x++) {
      if (vals[x] - vals[x-1] != vals[x-1] - vals[x-2]) { 
         return false; 
      }
   }
   return true;
    
}