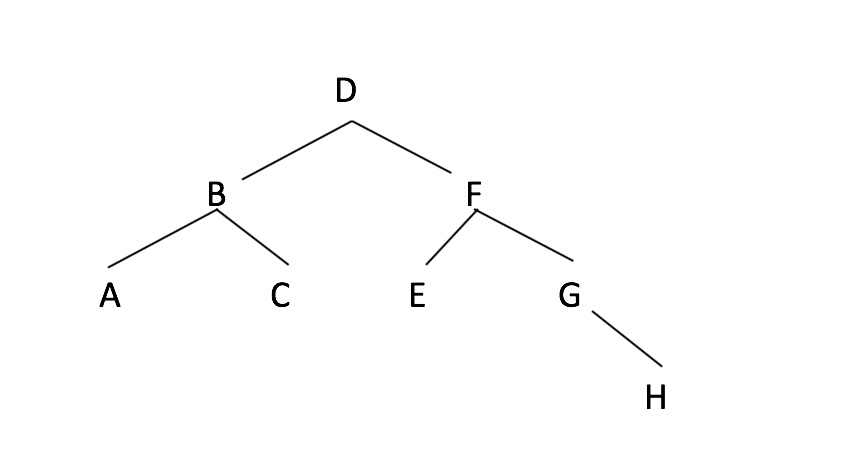
Problem 5 Rubric outline (8):
- -2 inconsistent computation of middle value
- -4 valid BST of keys A - H but not related binary search in this array.
- -8 not a valid BST (even if correct keys)
Problem 1 mergesort, binary search
Problem 1 Rubric (4):
-0.5 pts off for each one marked incorrectly of a - g
Problem 2
A. O(nlogn) B. O(log n) C. O(log n) D. O(n)
Problem 2 Rubric (8):
-2 for each incorrect answer
Problem 3
Many correct solutions (all look very similar).
Stack 1:
main mergesort merge <--- top
main mergesort mergesort merge <--- topProblem 3 Rubric outline (6):
public class MineField {
// define your mines variable here: (1)
Set<MineLoc> mines;
. . . // other constants and instance variables not shown
/**
Create a minefield with same dimensions as the given array,
and populate it with the mines in the array such that if
mineData[row][col] is true, then hasMine(row,col) will be true
and vice versa. . . . (other details left out)
@param mineData the data for the mines;
must have at least one row and one col.
*/
public MineField(boolean[][] mineData) {
initMines(mineData);
. . . [code to initialize the other instance variables not shown]
}
/**
Initializes the mines variable from mineData such that if
mineData[row][col] is true, then hasMine(row,col) will be true
and vice versa.
@param mineData the mine data; must have at least one row and one col.
*/
private void initMines(boolean[][] mineData) { // (2)
mines = new HashSet<MineLoc>();
for (int row = 0; row < mineData.length; row++) {
for (int col = 0; col < mineData[0].length; col++) {
if (mineData[row][col]) {
mines.add(new MineLoc(row, col));
}
}
}
}
/**
Returns whether there is a mine in this square
@param row row of the location to check
@param col column of the location to check
@return whether there is a mine in this square
PRE: inRange(row, col)
*/
public boolean hasMine(int row, int col) { // (3)
return mines.contains(new MineLoc(row, col));
}
// (4) any additional code
class MineLoc {
private int row;
private int col;
public MineLoc(int r, int c) {
row = r;
col = c;
}
}
Problem 4A Rubric outline (18):
(if you used a key that would not enable you to uniquely identify a
mine location, you lost all 4 points)
Problem 4B (2). O(1)
Problem 4C. O(1)
Problem 4C Rubric outline (2):
Problem 4D (2). VisibleField would not have to change at all.
Problem 5

Problem 5 Rubric outline (8):
Problem 6
There were many approaches. We'll show solutions for a few of them here.
Solution 1: 4-parameter helper with 2 reach-the-middle base cases
public boolean isUpDown(int[] a) {
return isUpDownR(a, 0, a.length-1, 1);
}
public boolean isUpDownR(int[] a, int low, int high, int curr) {
int len = high - low + 1;
boolean firstIsCurr = a[low] == curr;
if ((len == 1) && firstIsCurr) { return true; }
boolean firstIsLast = a[low] == a[high];
if ((len == 2) && firstIsCurr && firstIsLast) { return true; }
if ((!firstIsCurr) || (!firstIsLast)) { return false; }
return isUpDownR(a, low + 1, high - 1, curr + 1);
}
public boolean isUpDown(int[] a) {
return isUpDownR(a, 0);
}
public boolean isUpDownR(int[] a, int low) {
int high = a.length - low - 1;
if (low > high) { return true; } // the two values crossed
int curr = low + 1;
boolean firstIsCurr = a[low] == curr;
boolean firstIsLast = a[low] == a[high]; // when len==1 --> low==high
if ((!firstIsCurr) || (!firstIsLast)) { return false; }
return isUpDownR(a, low + 1);
}
public boolean isUpDown(int[] a) {
// have to check that the end values are 1 for this solution
if ((a[0] != 1) || (a[a.length-1] != 1)) {
return false;
}
return isUpDownR(a, 1); // pass in 1 bc going to compare with previous value
}
public boolean isUpDownR(int[] a, int low) {
int high = a.length - low - 1;
if (high < low) { return true; }
// check ascends by one and equal to the value in the same place on the other side
if (a[low] != a[low-1] + 1 || a[low] != a[high]) {
return false;
}
return isUpDownR(a, low + 1);
}