Final Review
As always, please interrupt at any time to ask questions!
Hashtables
Recall that maps associate a key with a value. In this week’s homework, you’re implementing a map using an AVL tree, which allows for insert, find, and remove functions to be performed in O(log n) time. That's pretty good, but can we do better?
Yes! Recall that a simple array maps an integer index to the value at that index: given an array arr and integer i, arr[i] returns the value stored at index i in constant time. A hash table (or an unordered map) takes advantage of this fact: it is implemented as an array that maps keys to their corresponding values. To make this possible, it requires a hash function, which converts keys into integer indices that can be used in the array.
Here’s an example: suppose you wanted to map a student’s name to their ID number. In this case, the hash function would take in a string, like “Michelle,” and output an integer, like 2, representing the index in the array in which the key, value pair
In what situations would you use an unordered map over an ordered one?
Note that a pretty serious problem arises when two unique keys map to the same index. We call these collisions, and we can handle them with either chaining or probing:
In chaining, each entry in the hash table is itself an array, linked list, or tree. What is the worst-case runtime for finding a key in a hash-table implemented with chaining?
In probing, if the location a key is hashed to is already occupied, we find another empty location to hash to. This means that if we want to find a key, we must first check the index given by the hash function. If the key is not at that index, we need to probe and move to the next spot. We know we can stop probing when we hit an empty location, but how do we differentiate between a location that was always empty, and one that used have a value? Why is this important?
Tries
How long does it take to search a balanced BST or a hash table with strings of k characters? In both cases, comparing key values requires comparing k-length strings. How much does it cost to compare two strings of length k?
As it turns out, searching a balanced BST with k-length strings takes Θ(k log n) time, while searching a hash table with k-length strings takes O(k) time. To see why, think about the work we need to do after we apply our hash function to our key. Once we have our index, how do we know if it holds our key-value pair? What do we do if there are collisions?
Tries are a data structure that guarantee O(k) retrieval AND no collisions. In a trie, each node holds a segment of a key (like a fragment of a string) and a bool indicating if it is a word node. A word node is one where the path from the root to the word node represents a full string or key. Here’s an example of a trie from Wikipedia:
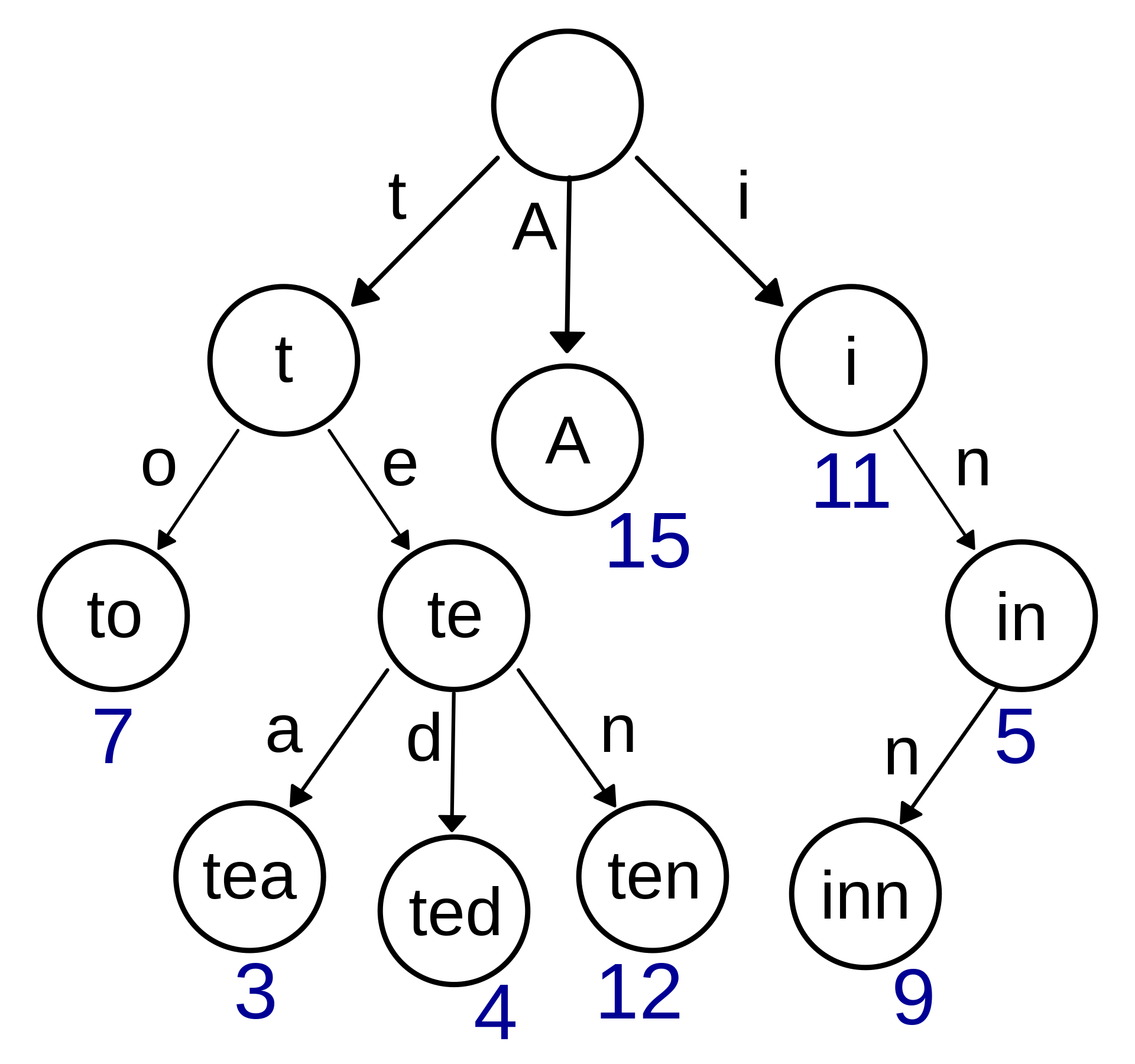
Suppose you wanted to find the key “tea.” You would start at the root and look for the first character, “t.” At each level, you will look for the next character fragment—“te,” followed by “tea.” How do you know when to stop searching? How do you know if the key you are looking for is not in the tree? Why do we need the bool?
Bloom Filters
Bloom filters are space-efficient data structures that can quickly tell you if an element is present in a map or set. There’s a trade-off: if you ask a bloom filter if a key is present, it will return yes or no, but by “yes,” it really means “maybe.” They are implemented as hash tables of single bits and multiple hash functions: to insert a key, simply apply the hash functions and set all corresponding indices to 1. To check if a key is in the bloom filter, apply all hash functions to the key and check if all corresponding indices contain 1. What might cause a false positive to occur? Why do we never get false negatives?
BST, AVL, and Splay Trees
Finally, let’s take a quick look at BST, AVL, and splay trees, which are the subjects of this week’s homework. As mentioned in the last lab, BSTs are a special kind of binary tree in which all values in the left subtree are less than or equal to the parent’s value, while all values in the right subtree are greater than or equal to the parent’s value. This makes inserting, removing, and finding within the tree very quick, if the tree height is small: most operations on a BST will take time that is proportional to the tree height. Given n nodes, what is the maximum height of a valid BST?
AVL & Splay Trees
AVL and splay trees are two examples of self-balancing trees that keep their operations fast. An AVL tree guarantees a height of O(log n) at all times, and we say that trees are height-balanced if the height difference between left and right subtrees <= 1. Unlike an AVL tree, the splay tree takes advantage of temporal locality by putting the most recently accessed item at the root. Knowing this, what is the runtime of accessing the most recently accessed item in a splay tree? What would it be if we had an AVL tree instead?
Programming Time! (Checkoff)
General tips for programming problems:
- Plan out what you're going to do before you start writing. It's probably helpful to jot down some pseudocode, see if it makes sense, and then start writing your answer.
- Run through some examples by hand. Once you have a solution, think of a few example inputs, and verify that your idea works. If you don't have a solution, going through examples by hand may help you develop one!
- Use descriptive and accurate variable/function names, and add comments if it's unclear what you're doing or why. You are way more likely to get points on the test if you do this.
- Don't write too much! If you find yourself filling up the entire page, or writing 3+ helper functions, you are likely overcomplicating the problem. There is a simpler solution, and you are almost certainly making it more difficult for your graders to understand what you're doing.
- If you're not sure how to do a problem, try to get partial credit! We'll give points for things like base cases and correct recursive calls, even if the rest of your code doesn't quite work. Try not to leave anything blank.
Binary Trie Insertion
With those tips in mind, let's implement insertion for a binary trie (aka a binary prefix tree).
In lecture, you've seen tries with edges for each letter in the alphabet — for binary tries, the only outgoing edges will be to '0' nodes and '1' nodes (node->zero and node->one). The insertion function is fairly close to the exists function (given), with one main difference.
Hashtable Implementation
You will be implementing a map of strings to ints using chaining. The hash function is already implemented, and you will be using the array of vector pointers to do the required functions.
That's all we have — thanks for a great semester!

